Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-18T06:58:16.927Z Has data issue: false hasContentIssue false
  • English
  • Français

DEGREES OF CATEGORICITY ON A CONE VIA η-SYSTEMS

Published online by Cambridge University Press:  21 March 2017

BARBARA F. CSIMA  and
MATTHEW HARRISON-TRAINOR
BARBARA F. CSIMA
Affiliation:
DEPARTMENT OF PURE MATHEMATICS UNIVERSITY OF WATERLOO 200 UNIVERSITY AVE. W. WATERLOO, ON N2L 3G1, CANADAE-mail: csima@uwaterloo.caURL: www.math.uwaterloo.ca/∼csima
MATTHEW HARRISON-TRAINOR
Affiliation:
GROUP IN LOGIC AND THE METHODOLOGY OF SCIENCE UNIVERSITY OF CALIFORNIA BERKELEY, CA 94720, USAE-mail: matthew.h-t@berkeley.eduURL: www.math.berkeley.edu/∼mattht
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the complexity of isomorphisms of computable structures on cones in the Turing degrees. We show that, on a cone, every structure has a strong degree of categoricity, and that degree of categoricity is 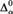${\rm{\Delta }}_\alpha ^0 $-complete for some α. To prove this, we extend Montalbán’s η-system framework to deal with limit ordinals in a more general way. We also show that, for any fixed computable structure, there is an ordinal α and a cone in the Turing degrees such that the exact complexity of computing an isomorphism between the given structure and another copy ${\cal B}$ in the cone is a c.e. degree in 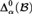${\rm{\Delta }}_\alpha ^0\left( {\cal B} \right)$. In each of our theorems the cone in question is clearly described in the beginning of the proof, so it is easy to see how the theorems can be viewed as general theorems with certain effectiveness conditions.

Keywords

computability theorycomputable structure theorydegrees of categoricitynatural structureon a cone
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 1 , March 2017 , pp. 325 - 346
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anderson, B. and Csima, B. F., Degrees that are not degrees of categoricity . Notre Dame Journal of Formal Logic, vol. 57 (2016), no. 3, pp. 389–398.Google Scholar
Ash, C. J., Recursive labelling systems and stability of recursive structures in hyperarithmetical degrees . Transactions of the American Mathematical Society, vol. 298 (1986), no. 2, pp. 497–514.Google Scholar
Ash, C. J., Stability of recursive structures in arithmetical degrees . Annals of Pure and Applied Logic, vol. 32 (1986), no. 2, pp. 113–135.CrossRefGoogle Scholar
Ash, C. J., Categoricity in hyperarithmetical degrees . Annals of Pure and Applied Logic, vol. 34 (1987), no. 1, pp. 1–14.Google Scholar
Ash, C. J., Labelling systems and r.e. structures . Annals of Pure and Applied Logic, vol. 47 (1990), no. 2, pp. 99–119.CrossRefGoogle Scholar
Ash, C. J. and Knight, J. F., Computable Structures and the Hyperarithmetical Hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, North-Holland, Amsterdam, 2000.Google Scholar
Ash, C. J., Knight, J. F., Manasse, M. S., and Slaman, T. A., Generic copies of countable structures . Annals of Pure and Applied Logic, vol. 42 (1989), no. 3, pp. 195–205.Google Scholar
Csima, B. F., Franklin, J. N. Y., and Shore, R. A., Degrees of categoricity and the hyperarithmetic hierarchy . Notre Dame Journal of Formal Logic, vol. 54 (2013), no. 2, pp. 215–231.Google Scholar
Chisholm, J., Effective model theory vs. recursive model theory, this Journal, vol. 55 (1990), no. 3, pp. 1168–1191.Google Scholar
Downey, R. G., Kach, A. M., Lempp, S., Lewis-Pye, A. E. M., Montalbán, A., and Turetsky, D. D., The complexity of computable categoricity . Advances in Mathematics, vol. 268 (2015), pp. 423–466.CrossRefGoogle Scholar
Fokina, E., Frolov, A., and Kalimullin, I., Categoricity spectra for rigid structures . Notre Dame Journal of Formal Logic, vol. 57 (2016), no. 1, pp. 45–57.Google Scholar
Fokina, E. B., Kalimullin, I., and Miller, R., Degrees of categoricity of computable structures . Archive for Mathematical Logic, vol. 49 (2010), no. 1, pp. 51–67.Google Scholar
Goncharov, S. S., Autostability and computable families of constructivizations . Algebra and Logic, vol. 14 (1975), no. 6, pp. 392–409 (In Russian).Google Scholar
Goncharov, S. S., The number of nonautoequivalent constructivizations . Algebra and Logic, vol. 16 (1977), no. 3, pp. 257–282, 377 (In Russian).Google Scholar
Goncharov, S. S. and Dzgoev, V. D., Autostability of models . Algebra and Logic, vol. 19 (1980), no. 1, pp. 28–37 (In Russian).Google Scholar
Goncharov, S. S., Harizanov, V. S., Knight, J. F., McCoy, C. F. D., Miller, R. G., and Solomon, R., Enumerations in computable structure theory . Annals of Pure and Applied Logic, vol. 136 (2005), no. 3, pp. 219–246.Google Scholar
Harizanov, V., Some effects of Ash-Nerode and other decidability conditions on degree spectra . Annals of Pure and Applied Logic, vol. 55 (1991), no. 1, pp. 51–65.Google Scholar
Harrison-Trainor, M., Degree spectra of relations on a cone . Memoirs of the American Mathematical Society, to appear.Google Scholar
Knight, J. F., Degrees coded in jumps of orderings, this Journal, vol. 51 (1986), no. 4, pp. 1034–1042.Google Scholar
Martin, D. A., The axiom of determinateness and reduction principles in the analytical hierarchy . Bulletin of the American Mathematical Society, vol. 74 (1968), pp. 687–689.Google Scholar
Martin, D. A., Borel determinacy . Annals of Mathematics (2), vol. 102 (1975), no. 2, pp. 363–371.Google Scholar
McCoy, C. F. D., Finite computable dimension does not relativize . Archive for Mathematical Logic, vol. 41 (2002), no. 4, pp. 309–320.CrossRefGoogle Scholar
Miller, R., d-computable categoricity for algebraic fields, this Journal, vol. 74 (2009), no. 4, pp. 1325–1351.Google Scholar
Montalbán, A., Priority arguments via true stages, this Journal, vol. 79 (2014), no. 4, pp. 1315–1335.Google Scholar
Montalbán, A., A robuster Scott rank . Proceedings of the American Mathematical Society, vol. 143 (2015), no. 12, pp. 5427–5436.Google Scholar
Remmel, J. B., Recursively categorical linear orderings . Proceedings of the American Mathematical Society, vol. 83 (1981), no. 2, pp. 387–391.Google Scholar
Scott, D., Logic with denumerably long formulas and finite strings of quantifiers , Theory of Models (Proceedings of the 1963 International Symposium at Berkeley), North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar