Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-24T04:04:23.310Z Has data issue: false hasContentIssue false
  • English
  • Français

ABSTRACT ω-LIMIT SETS

Published online by Cambridge University Press:  01 August 2018

WILL BRIAN
WILL BRIAN*
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF NORTH CAROLINA AT CHARLOTTE 9201 UNIVERSITY CITY BLVD. CHARLOTTE, NC 28223-0001, USAE-mail:wbrian.math@gmail.comURL: wrbrian.wordpress.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The shift map σ on ω* is the continuous self-map of ω* induced by the function n ↦ n + 1 on ω. Given a compact Hausdorff space X and a continuous function f : X → X, we say that (X, f) is a quotient of (ω*, σ) whenever there is a continuous surjection Q : ω*→ X such that Q ○ σ = σ ○ f.

Our main theorem states that if the weight of X is at most ℵ1, then (X, f) is a quotient of (ω*, σ), if and only if f is weakly incompressible (which means that no nontrivial open U ⊆ X has 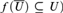$f\left( {\bar{U}} \right) \subseteq U$). Under CH, this gives a complete characterization of the quotients of (ω*, σ) and implies, for example, that (ω*, σ−1) is a quotient of (ω*, σ).

In the language of topological dynamics, our theorem states that a dynamical system of weight ℵ1 is an abstract ω-limit set if and only if it is weakly incompressible.

We complement these results by proving (1) our main theorem remains true when ℵ1 is replaced by any κ < p, (2) consistently, the theorem becomes false if we replace ℵ1 by ℵ2, and (3) OCA + MA implies that (ω*, σ−1) is not a quotient of (ω*, σ).

Keywords

Primary 54H20Secondary03C9803E3537B0554G05Stone–Čech compactificationshift mapParovičenko’s theoremabstract omega-limit setsweak incompressibilityContinuum Hypothesiselementary submodelsMartin’s Axiom
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 2 , June 2018 , pp. 477 - 495
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akin, E., The General Topology of Dynamical Systems, Graduate Studies in Mathematics, reprint edition, American Mathematical Society, Providence, RI, 2010.CrossRefGoogle Scholar
Barwell, A. D., Good, C., Oprocha, P., and Raines, B. E., Characterizations of ω-limit sets of topologically hyperbolic spaces. Discrete and Continuous Dynamical Systems, vol. 33 (2013), no. 5, pp. 1819–1833.CrossRefGoogle Scholar
Bell, M., On the combinatorial principle P(c). Fundamenta Mathematicae, vol. 114 (1981), no. 2, pp. 149–157.CrossRefGoogle Scholar
Blass, A., Ultrafilters: Where topological dynamics = algebra = combinatorics. Topology Proceedings, vol. 18 (1993), pp. 33–56.Google Scholar
Błaszczyk, A. and Szymański, A., Concerning Parovičenko’s theorem. Bulletin de L’Academie Polonaise des Sciences Série des sciences mathématiques, vol. 28 (1980), no. 7-8, pp. 311–314.Google Scholar
Bowen, R., ω-limit sets for axiom A diffeomorphisms. Journal of Differential Equations, vol. 18 (1975), no. 2, pp. 333–339.CrossRefGoogle Scholar
Brian, W. R., P-sets and minimal right ideals in ℕ*. Fundamenta Mathematicae, vol. 229 (2015), no. 3, pp. 277–293.CrossRefGoogle Scholar
van Douwen, E. K. and Przymusiński, T. C., Separable extensions of first-countable spaces. Fundamenta Mathematicae, vol. 111 (1980), pp. 147–158.CrossRefGoogle Scholar
Dow, A. and Hart, K. P. A universal continuum of weight ℵ. Transactions of the American Mathematical Society, vol. 353 (2000), no. 5, pp. 1819–1838.CrossRefGoogle Scholar
Engelking, R., General Topology, revised ed., Sigma Series in Pure Mathematics, vol. 6, Heldermann, Berlin, 1989.Google Scholar
Farah, I., Analytic quotients: Theory of lifting for quotients over analytic ideals on the integers. Memoirs of the American Mathematical Society, vol. 148 (2000), no. 702, pp. 1–177.CrossRefGoogle Scholar
Farah, I., The fourth head of β ℕ, Open Problems in Topology II (Pearl, E., editor), Elsevier, Amsterdam, 2007, pp. 145–150.Google Scholar
Geschke, S., The shift on ${\cal P}\left( \omega \right)/{\rm{fin}}$, unpublished manuscript. Available at www.math.uni-hamburg.de/home/geschke/publikationen.html.en.Google Scholar
Hindman, N. and Strauss, D., Algebra in the Stone-Čech Compactification, second ed., De Gruyter, Berlin, 2012.Google Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, vol. 42, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Larson, P. and McKenney, P., Automorphisms of ${\cal P}\left( \lambda \right)/{{\cal I}_\kappa }$.. Fundamenta Mathematicae, vol. 233 (2016), no. 3, pp. 271–291.Google Scholar
Meddaugh, J. and Raines, B. E., Shadowing and internal chain transitivity. Fundamenta Mathematicae, vol. 222 (2013), no. 3, pp. 279–287.CrossRefGoogle Scholar
van Mill, J, An introduction to βω, Handbook of Set-Theoretic Topology (Kunen, K. and Vaughan, J. E., editors), North-Holland, Amsterdam, 1984, pp. 503–560.CrossRefGoogle Scholar
Noble, N. and Ulmer, M., Factoring functions on Cartesian products. Transactions of the American Mathematical Society, vol. 163 (1972), pp. 329–339.CrossRefGoogle Scholar
Parovičenko, I. I., A universal bicompact of weight ℵ1. Soviet Mathematics Doklady, vol. 4 (1963), pp. 592–595.Google Scholar
Sharkovsky, O. M., On attracting and attracted sets. Doklady Akademii Nauk SSSR, vol. 160 (1965), pp. 1036–1038.Google Scholar
Shchepin, E. V., Real functions and canonical sets in Tikhonov products and topological groups. Russian Mathematical Surveys, vol. 31 (1976), no. 6, pp. 17–27.CrossRefGoogle Scholar
Shelah, S., Proper Forcing, Lecture Notes in Mathematics, vol. 940, Springer-Verlag, Berlin, 1982.CrossRefGoogle Scholar
Shelah, S. and Steprāns, J., PFA implies all automorphisms are trivial. Proceedings of the American Mathematical Society, vol. 104 (1988), no. 4, pp. 1220–1225.CrossRefGoogle Scholar
Velickovic, B., OCA and automorphisms of ${\cal P}\left( \omega \right)/{\rm{fin}}$.. Topology and its Applications, vol. 49 (1992), no. 1, pp. 1–12.CrossRefGoogle Scholar