We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 15 February 2021
For every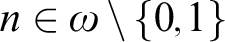 
$n\in \omega \setminus \{0,1\}$
we introduce the
following weak choice principle:
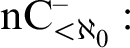$\operatorname {nC}_{<\aleph _0}^-:$
For every infinite family
$\mathcal {F}$
of finite sets of size at least n there is an infinite subfamily
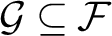$\mathcal {G}\subseteq \mathcal {F}$
with a selection function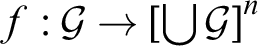
$f:\mathcal {G}\to \left [\bigcup \mathcal {G}\right ]^n$
such that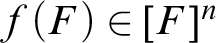
$f(F)\in [F]^n$
for all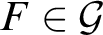
$F\in \mathcal {G}$
.
Moreover, we consider the following choice principle:
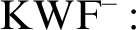$\operatorname {KWF}^-:$
For every infinite family
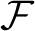$\mathcal {F}$
of finite sets of size at least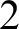
$2$
there is an infinite subfamily
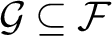$\mathcal {G}\subseteq \mathcal {F}$
with a Kinna–Wagner selection function. That is, there is a function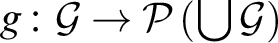
$g\colon \mathcal {G}\to \mathcal {P}\left (\bigcup \mathcal {G}\right )$
with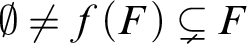
$\emptyset \not =f(F)\subsetneq F$
for every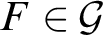
$F\in \mathcal {G}$
.
We will discuss the relations between these two choice principles and their relations to other well-known weak choice principles. Moreover, we will discuss what happens when we replace
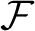$\mathcal {F}$
by a linearly ordered or a well-ordered family.
