Article contents
Theoretical Pearls: Self-interpretation in lambda calculus
Published online by Cambridge University Press: 10 August 2016
Extract
Programming languages which are capable of interpreting themselves have been fascinating computer scientists. Indeed, if this is possible then a ‘strange loop’ (in the sense of Hofstadter, 1979) is involved. Nevertheless, the phenomenon is a direct consequence of the existence of universal languages. Indeed, if all computable functions can be captured by a language, then so can the particular job of interpreting the code of a program of that language. Self-interpretation will be shown here to be possible in lambda calculus.
The set of λ-terms, notation Λ, is defined by the following abstract syntax
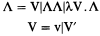
where
is the set {v, v′, v″, v′″,…} of variables. Arbitrary variables are usually denoted by x, y,z,… and λ-terms by M,N,L,…. A redex is a λ-term of the form
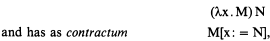
that is, the result of substituting N for (the free occurrences of) x in M. Stylistically, it can be said that λ-terms represent functional programs including their input. A reduction machine executes such terms by trying to reduce them to normal form; that is, redexes are continuously replaced by their contracta until hopefully no more redexes are present. If such a normal form can be reached, then this is the output of the functional program; otherwise, the program diverges.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1991
References
- 22
- Cited by





Discussions
No Discussions have been published for this article.