Skip to main content
SpringerLink
Log in

A priori Probability That Two Qubits Are Unentangled

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

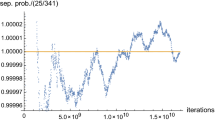
In a previous study (P. B. Slater, Eur. Phys. J. B. 17, 471 (2000)), several remarkably simple exact results were found, in certain specialized m-dimensional scenarios (m ≤ 4), for the a priori probability that a pair of qubits is unentangled/separable. The measure used was the volume element of the Bures metric (identically one-fourth the statistical distinguishability [SD] metric). Here, making use of a newly-developed (Euler angle) parameterization of the 4 × 4 density matrices of Tilma, Byrd and Sudarshan, we extend the analysis to the complete 15-dimensional convex set (C) of arbitrarily paired qubits—the total SD volume of which is known to be π8 / 1680 = π8/24 ⋅ 3 ⋅ 5 ⋅ 7 ≈ 5.64794. Using advanced quasi-Monte Carlo procedures (scrambled Halton sequences) for numerical integration in this high-dimensional space, we approximately (5.64851) reproduce that value, while obtaining an estimate of 0.416302 for the SD volume of separable states. We conjecture that this is but an approximation to π6/2310 = π6 / (2 ⋅ 3 ⋅ 5 ⋅ 7 ⋅ 11) ≈ 0.416186. The ratio of the two volumes, 8/11π22 ≈ .0736881, would then constitute the exact Bures/SD probability of separability. The SD area of the 14-dimensional boundary of C is 142π7/12285 = 2 ⋅ 71π7/33 ⋅ 5 ⋅ 7 ⋅ 13 ≈ 34.911, while we obtain a numerical estimate of 1.75414 for the SD area of the boundary of separable states.

PACS: 03.67.-; 03.65.Ud; 02.60.Jh; 02.40.Ky

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

REFERENCES

  1. K. ?yczkowski, P. Horodecki, A. Sanpera, and M. Lewenstein Phys. Rev. A 58, 883 (1998).

    Google Scholar 

  2. K. ?yczkowski, Phys. Rev. A 60, 3496 (1999).

    Google Scholar 

  3. K. ?yczkowski and H. J. Sommers, J. Phys. A 34, 7111 (2001).

    Google Scholar 

  4. P. B. Slater, J. Phys. A 32, 5261 (1999).

    Google Scholar 

  5. P. B. Slater, Eur. Phys. J. B 17, 471 (2000).

    Google Scholar 

  6. R. E. Kass, Statist. Sci. 4, 188 (1989).

    Google Scholar 

  7. M. Hübner, Phys. Lett. A 163, 239 (1992).

    Google Scholar 

  8. M. Hübner, Phys. Lett. A 179, 221 (1993).

    Google Scholar 

  9. S. L. Braunstein and C. M. Caves, Phys. Rev. Lett. 72, 3439 (1994).

    Google Scholar 

  10. P. B. Slater, J. Geom. Phys. 39, 207 (2001).

    Google Scholar 

  11. J. Dittmann, J. Phys. A 32, 2663 (1999).

    Google Scholar 

  12. L. C. Kwek, C. H. Oh, and X.-B. Wang, J. Phys. A 32, 6613 (1999).

    Google Scholar 

  13. A. A. Holevo, Statistical Structure of Quantum Theory (Springer, Berlin, 2001).

    Google Scholar 

  14. M. J. W. Hall, Phys. Lett. A 242, 123 (1998).

    Google Scholar 

  15. J. Dittmann, Lett. Math. Phys. 46, 281 (1998).

    Google Scholar 

  16. P. B. Slater, math-ph/0108005.

  17. J.-L. Chen, L. Fu, A. A. Ungar, and X.-G. Zhao, Phys. Rev. A 65, 024303 (2002).

    Google Scholar 

  18. D. Petz and C. SÚdar, J. Math. Phys. 37, 2662 (1996).

    Google Scholar 

  19. G. Vidal, W. Dür, and J. I. Cirac, Phys. Rev. Lett. 89, 027901 (2002).

    Google Scholar 

  20. J. Matoušek, Geometric Discrepancy (Springer, Berlin).

  21. H. Faure, J. Number Theory 42, 47 (1992).

    Google Scholar 

  22. G. Ökten, MATHEMATICA in Educ. Res. 8, 52 (1999).

    Google Scholar 

  23. R. F. Werner, Phys. Rev. A 40, 4277 (1989).

    Google Scholar 

  24. M. Horodecki, P. Horodecki, and R. Horodecki, Phys. Rev. Lett. 80, 5239 (1998).

    Google Scholar 

  25. V. Vedral, Phys. Lett. A 262, 121 (1999).

    Google Scholar 

  26. V. Vedral and M. B. Plenio, Phys. Rev. A 57, 1619 (1998).

    Google Scholar 

  27. R. A. Bertlmann, N. Narnhofer, and W. Thirring, Phys. Rev. A 66, 032319 (2002).

    Google Scholar 

  28. X.-B. Wang, L. C. Kwek, and C. H. Oh, J. Phys. A 33, 4925 (2000).

    Google Scholar 

  29. J.-L. Chen, L. Fu, A. A. Ungar, and X.-G. Zhao, Phys. Rev. A 6502, U822 (2002).

    Google Scholar 

  30. V. E. Mkrtchian and V. O. Chaltykian, Opt. Commun., 63, 239 (1987).

    Google Scholar 

  31. U. Fano, Rev. Mod. Phys. 55, 855 (1983).

    Google Scholar 

  32. F. J. Bloore, J. Phys. A 9, 2059 (1976).

    Google Scholar 

  33. P. B. Slater, J. Opt. B: Quantum Semiclass. Opt. 2, L19 (2000).

    Google Scholar 

  34. T. Tilma, M. S. Byrd, and E. C. G. Sudarshan, J. Phys. A 35, 10445 (2002).

    Google Scholar 

  35. P. B. Slater, quant-ph/0203088v1.

  36. M. S. Byrd and P. B. Slater, Phys. Lett. A 283, 152 (2001).

    Google Scholar 

  37. P. B. Slater, J. Opt. B 2, L19 (2000).

    Google Scholar 

  38. P. B. Slater, J. Phys. A 32, 8231 (1999).

    Google Scholar 

  39. A. Peres, Phys. Rev. Lett. 77, 1413 (1996).

    Google Scholar 

  40. M. Horodecki, P. Horodecki, and R. Horodecki, Phys. Lett. A 223, 1 (1996).

    Google Scholar 

  41. F. Verstraete, J. Dehaene, and B. De Moor, Phys. Rev. A 6401, U3 (2001).

    Google Scholar 

  42. A. Sanpera, R. Tarrach, and G. Vidal, Phys. Rev. A 58, 826 (1998).

    Google Scholar 

  43. A. O. Pittenger and A. O. Rubin, Lin. Alg. Appl. 346, 47 (2002).

    Google Scholar 

  44. A. M. Wang, quant-ph/0002073.

  45. N. J. A. Sloane, The On-Line Encyclopaedia of Integer Sequences, www.research.att.com/njas/sequences/index.html.

  46. F. Verstraete, K. Audenaert, and J. Dehaene, J. Phys. A 34, 10327 (2001).

    Google Scholar 

  47. F. Verstraete, J. Dehaene, and B. De Moor, J. Mod. Opt. 49, 1277 (2002).

    Google Scholar 

  48. C. K. Caldwell, Math. Comput. 64, 889 (1995).

    Google Scholar 

  49. M. Byrd and E. C. G. Sudarshan, J. Phys. A 31, 9255 (1998).

    Google Scholar 

  50. P. B. Slater, quant-ph/0211150.

  51. T. Tilma and E. C. G. Sudarshan, J. Phys. A 35, 10467 (2002).

    Google Scholar 

  52. D. P. DiVincenzo, B. M. Terhal, and A. V. Thapliyal, J. Mod. Opt. 47, 377 (2000).

    Google Scholar 

  53. I. Chavel, Isoperimetric Inequalities: Differential Geometric and Analytic Perspectives (Cambridge University Press, Cambridge, 2001).

    Google Scholar 

  54. F. Morgan and D. L. Johnson, Indiana Univ. Math. J. 49, 1017 (2000).

    Google Scholar 

  55. O. Druet, Proc. Amer. Math. Soc. 130, 2351 (2002).

    Google Scholar 

  56. O. Druet, Geom. Dedicata 90, 217 (2002).

    Google Scholar 

  57. J. Dittmann, Sem Sophus Lie 3, 73 (1993).

    Google Scholar 

  58. J. Dittmann, J. Geom. Phys. 31, 16 (1999).

    Google Scholar 

  59. J. Dittmann, Lin. Algebra Appl. 315, 83 (2000).

    Google Scholar 

  60. J. Dittmann, J. Lie Theory 3, 73 (1993).

    Google Scholar 

  61. D. E. Vol'per, Siberian Math. J. 38, 223 (1997).

    Google Scholar 

  62. M. Gromov, Metric Structures for Riemannian and Non-Riemannian Spaces (Birkhauser, Boston, 1999).

    Google Scholar 

  63. I. Chavel, Riemannian Geometry-A Modern Introduction (Cambridge University Press, Cambridge, 1993).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. ISBER, University of California, Santa Barbara, California, 93106-2150

    Paul B. Slater

Authors
  1. Paul B. Slater
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Slater, P.B. A priori Probability That Two Qubits Are Unentangled. Quantum Information Processing 1, 397–408 (2002). https://doi.org/10.1023/A:1023421914825

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1023421914825

Search

Navigation