Skip to main content
SpringerLink
Log in

A heavy traffic limit theorem for a class of open queueing networks with finite buffers

  • Published:
Queueing Systems Aims and scope Submit manuscript

Abstract

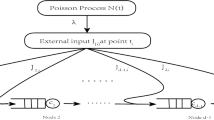
We consider a queueing network of d single server stations. Each station has a finite capacity waiting buffer, and all customers served at a station are homogeneous in terms of service requirements and routing. The routing is assumed to be deterministic and hence feedforward. A server stops working when the downstream buffer is full. We show that a properly normalized d-dimensional queue length process converges in distribution to a fd-dimensional semimartingale reflecting Brownian motion (RBM) in a d-dimensional box under a heavy traffic condition. The conventional continuous mapping approach does not apply here because the solution to our Skorohod problem may not be unique. Our proof relies heavily on a uniform oscillation result for solutions to a family of Skorohod problems. The oscillation result is proved in a general form that may be of independent interest. It has the potential to be used as an important ingredient in establishing heavy traffic limit theorems for general finite buffer networks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. Bardhan and S. Mithal, Heavy-traffic limits for an open network of finite-buffer overflow queues: The single class case, preprint (1993).

  2. A. Bernard and A. El Kharroubi, Régulations déterministes et stochastiques dans le premier “orthant” de Rn, Stochastics Stochastics Rep. 34(1991) 149–167.

    Google Scholar 

  3. D. Bertsekas and R. Gallagher, Data Networks (Prentice-Hall, Englewood Cliffs, NJ, 1992).

    Google Scholar 

  4. P. Billingsley, Convergence of Probability Measures (Wiley, New York, 1968).

    Google Scholar 

  5. M. Bramson, Convergence to equilibria for fluid models of FIFO queueing networks, Queueing Systems 22(1996) 5–45.

    Article  Google Scholar 

  6. M. Bramson, Convergence to equilibria for fluid models of head-of-the-line proportional processor sharing queueing networks, Queueing Systems 23(1997) 1–26.

    Article  Google Scholar 

  7. M. Bramson, State space collapse with application to heavy traffic limits for multiclass queueing networks, Queueing Systems 30(1998) 89–148.

    Article  Google Scholar 

  8. A. Brondstred, An Introduction to Convex Polytopes (Springer, New York, 1983).

    Google Scholar 

  9. J.A. Buzacott, Automatic transfer lines with buffer stocks, Internat. J. Prod. Res. 5(1967) 183–200.

    Google Scholar 

  10. H. Chen and H. Zhang, Stability of multiclass queueing networks under FIFO service discipline, Math. Oper. Res. 22(1997) 691–725.

    Google Scholar 

  11. H. Chen and H. Zhang, Diffusion approximations for multiclass FIFO queueing networks, preprint.

  12. D.W. Cheng, Second order properties in a tandem queue with general blocking, Oper. Res. Lett. 12 (1992) 139–144.

    Article  Google Scholar 

  13. D. Cheng and D.D. Yao, Tandem queues with general blocking: A unified model and comparison results, Discrete Event Dyn. Systems 2(1993) 207–234.

    Article  Google Scholar 

  14. K.L. Chung and J.R. Williams, Introduction to Stochastic Integration (Birkhäuser, Boston, 1983).

    Google Scholar 

  15. J.G. Dai and J.M. Harrison, Steady-state analysis of RBM in a rectangle: Numerical methods and a queueing application, Ann. Appl. Probab. 1(1991) 16–35.

    Google Scholar 

  16. J.G. Dai and T.G. Kurtz, A multiclass station with Markovian feedback in heavy traffic, Math. Oper. Res. 20(1995) 721–742.

    Google Scholar 

  17. J.G. Dai, G. Wang and Y. Wang, Nonuniqueness of the Skorohod problem arising from FIFO Kelly type network, private communication (1992).

  18. J.G. Dai and R.J.Williams, Existence and uniqueness of semimartingale reflecting Brownian motions in convex polyhedrons, Theory Probab. Appl. 40(1995) 3–53.

    Article  Google Scholar 

  19. W. Dai, Brownian approximations for queueing networks with finite buffers: modeling, heavy traffic analysis and numerical implementations, Ph.D. thesis, School of Mathematics, Georgia Institute of Technology (1996).

  20. A.I. Elwalid and D. Mitra, Analysis and design of rate-based congestion control of high speed networks, I: Stochastic fluid models, access regulation, Queueing Systems 9(1991) 29–64.

    Article  Google Scholar 

  21. S.N. Ethier and T.G. Kurtz, Markov Processes: Characterization and Convergence (Wiley, New York, 1986).

    Google Scholar 

  22. L.M. Graves, The Theory of Functions of Real Variables (McGraw-Hill, New York, 1956).

    Google Scholar 

  23. A. Gut, Stopped Random Walks: Limit Theorems and Applications (Springer, Berlin, 1988).

    Google Scholar 

  24. J.M. Harrison, Brownian models of queueing networks with heterogeneous customer populations, in: Proc.of the IMA Workshop on Stochastic Differential Systems (Springer, Berlin, 1988).

    Google Scholar 

  25. D.L. Iglehart and W. Whitt, Multiple channel queues in heavy traffic I, Adv. in Appl. Probab. 2 (1970) 150–177.

    Article  Google Scholar 

  26. D.L. Iglehart and W. Whitt, Multiple channel queues in heavy traffic II, Adv. in Appl. Probab. 2 (1970) 355–364.

    Article  Google Scholar 

  27. D.P. Johnson, Diffusion approximations for optimal filtering of jump processes and for queueing networks, Ph.D. thesis, University of Wisconsin (1983).

  28. T. Konstantopoulos and J. Walrand, On the ergodicity of networks of /GI/1/N queues, Adv. in Appl. Probab. 22(1990) 263–267.

    Article  Google Scholar 

  29. H. Kroner, M. Eberspacher, T.H. Theimer, P.J. Kuhn and U. Briem, Approximate analysis of the end to end delay in ATM networks, in: Proc.of the IEEE INFOCOM’ 92, Florence, Italy (1992) pp. 978–986.

  30. G. Last and A. Brandt, Marked Point Processes on the Real Line: The Dynamic Approach (Springer, New York, 1995).

    Google Scholar 

  31. D. Mitra and I. Mitrani, Analysis of a Kanban discipline for cell coordination in production lines: I, Managm. Sci.36(1990) 1458–1566.

    Google Scholar 

  32. H. Perros and T. Altiok, Queueing networks with blocking: A bibliography, Performance Evaluation Rev.: ACM Sigmetrics 12(1984) 8–12.

    Google Scholar 

  33. W.P. Peterson, A heavy traffic limit theorem for networks of queues with multiple customer types, Math. Oper. Res. 16(1991) 90–118.

    Article  Google Scholar 

  34. M.I. Reiman, Open queueing networks in heavy traffic, Math. Oper. Res. 9(1984) 441–458.

    Google Scholar 

  35. M.I. Reiman, A multiclass feedback queue in heavy traffic, Adv. in Appl. Probab. 20(1988) 179–207.

    Article  Google Scholar 

  36. M.I. Reiman and R.J. Williams, A boundary property of semimartingale reflecting Brownian motions, Probab. Theory Related Fields 77(1988) 87–97and 80 (1989) 633.

    Article  Google Scholar 

  37. L.M. Taylor and R.J. Williams, Existence and uniqueness of semimartingale reflecting Brownian motions in an orthant, Probab. Theory Related Fields 96(1993) 283–317.

    Article  Google Scholar 

  38. R.J.Williams, An invariance principle for semimartingale reflecting Brownian motions in an orthant, Queueing Systems 30(1998) 5–25.

    Article  Google Scholar 

  39. R.J. Williams, Diffusion approximations for open multiclass queueing networks: Sufficient conditions involving state space collapse, Queueing Systems 30(1998) 27–88.

    Article  Google Scholar 

  40. D.D. Yao, Probability Models in Manufacturing Systems, Springer Series in Operations Research (Springer, Berlin, 1994).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Industrial and Systems Engineering, and School of Mathematics, Georgia Institute of Technology, Atlanta, GA, 30332-0205, USA

    J.G. Dai

  2. School of Mathematics, Georgia Institute of Technology, Atlanta, GA, 30332-0160, USA

    W. Dai

Authors
  1. J.G. Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. W. Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dai, J., Dai, W. A heavy traffic limit theorem for a class of open queueing networks with finite buffers. Queueing Systems 32, 5–40 (1999). https://doi.org/10.1023/A:1019178802391

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1019178802391

Search

Navigation