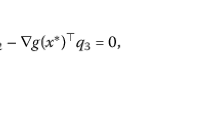Abstract
As shown by an example, the integral function f :ℝn → ℝ, defined by f(x) = ∫a b[B(x, t)]+ g(t) dt, may not be a strongly semismooth function, even if g(t) ≡ 1 and B is a quadratic polynomial with respect to t and infinitely many times smooth with respect to x. We show that f is a strongly semismooth function if g is continuous and B is affine with respect to t and strongly semismooth with respect to x, i.e., B(x, t) = u(x)t + v(x), where u and v are two strongly semismooth functions in ℝn. We also show that f is not a piecewise smooth function if u and v are two linearly independent linear functions, g is continuous and g ≢ 0 in [a, b], and n ≥ 2. We apply the first result to the edge convex minimum norm network interpolation problem, which is a two-dimensional interpolation problem.
Similar content being viewed by others
References
A. Agrachev, D. Pallaschke, and S. Scholtes, “On Morse theory for piecewise smooth functions,” J. Dynam. Control Sys., vol. 3, pp. 449-469, 1997.
L.-E. Andersson and T. Elfving, “An algorithm for constrained interpolation,” SIAM J. Sci. Statist. Comput., vol. 8, pp. 1012-1025, 1987.
L.-E. Andersson, T. Elfving, G. Iliev, and K. Vlachkova, “Interpolation of convex scattered data in R3 based upon an edged convex minimum norm network,” J. Approx. Theory., vol. 80, pp. 299-320, 1995.
X. Chen, L. Qi, and D. Sun, “Global and superlinear convergence of the smoothing Newton method and its application to general box constrained variational inequalities,” Math. Comput., vol. 67, pp. 519-540, 1998.
F.H. Clarke, Optimization and Nonsmooth Analysis, John Wiley & Sons: New York, 1983. (Reprinted by SIAM, Philadelphia, PA, 1990.)
S.L. Dodd, D.F. McAllister, and J.A. Roulier, “Shape-preserving spline interpolation for specifying bivariate functions on grids,” IEEE Comput. Graph. Appl., vol. 3, pp. 70-79, 1983.
A.L. Dontchev and W.W. Hager, “Implicit functions, Lipschitz maps, and stability in optimization,” Math. Oper. Res., vol. 19, pp. 753-768, 1994.
A.L. Dontchev and B.D. Kalchev, “Duality and well-posedness in convex interpolation,” Numer. Funct. Anal. and Optim., vol. 10, pp. 673-689, 1989.
A.L. Dontchev, H.-D. Qi, and L. Qi, “Convergence of Newton's method for convex best interpolation,” Numer. Math., vol. 87, pp. 435-456, 2001.
A.L. Dontchev, H.-D. Qi, and L. Qi, “Quadratic convergence of Newton's method for convex interpolation and smoothing,” Constr. Approx., vol. 19, pp. 123-143, 2003.
A.L. Dontchev, H.-D. Qi, L. Qi, and H. Yin, “A Newton method for shapepreserving spline interpolation,” SIAM J. Optim., vol. 13, pp. 588-602, 2003.
F. Facchinei, A. Fischer, and C. Kanzow, “Regularity properties of a semismooth reformulation of variational inequalities,” SIAM J. Optim., vol. 8, pp. 850-869, 1998.
A. Fischer, “Solution of monotone complementarity problems with locally Lipschitzian functions,” Math. Prog., vol. 76, pp. 513-532, 1997.
M. Fukushima and L. Qi, “Reformulation: Nonsmooth, piecewise smooth, semismooth and smoothing methods,” Applied Optimization 22, Kluwer Academic Publishers, Dordrecht, 1999.
L.D. Irvine, S.P. Marin, and P.W. Smith, “Constrained interpolation and smoothing,” Constr. Approx., vol. 2, pp. 129-151, 1986.
H. Jiang and L. Qi, “Local uniqueness and Newton-type methods for nonsmooth variational inequalities,” J. Math. Analysis and Appl., vol. 196, pp. 314-331, 1995.
H. Jiang, L. Qi, X. Chen, and D. Sun, “Semismoothness and superlinear convergence in nonsmooth optimization and nonsmooth equations,” Nonlinear Optimization and Applications (Erice, 1995), 197-212, G. Di Pillo and F. Giannessi (Eds.), Plenum Publishing Corporation, New York, 1996.
C. Kanzow and H. Kleinmichel, “A new class of semismooth Newton-type methods for nonlinear complementarity problems,” Comput. Optim. Appl., vol. 11, pp. 227-251, 1998.
C.A. Micchelli, P.W. Smith, J. Swetits, and J.D. Ward, “Constrained L p approximation,” Constr. Approx., vol. 1, pp. 93-102, 1985.
C.A. Micchelli and F.I. Utreras, “Smoothing and interpolation in a convex subset of a Hilbert space,” SIAM J. Sci. Statist. Comput., vol. 9, pp. 728-747, 1988.
R. Mifflin, “Semismoothness and semiconvex functions in constrained optimization,” SIAM J. Control Optim., vol. 15, pp. 959-972, 1977.
G.M. Nielson, “A method for interpolating scattered data based upon a minimum norm network,” Math. Comp., vol. 40, pp. 253-271, 1983.
J.-S. Pang and D. Ralph, “Piecewise smoothness, local invertibility, and parametric analysis of normal maps,” Math. Oper. Res., vol. 21, pp. 401-426, 1996.
L. Qi, “Convergence analysis of some algorithms for solving nonsmooth equations,” Math. Oper. Res., vol. 18, pp. 227-253, 1993.
L. Qi and H. Jiang, “Semismooth Karush-Kuhn-Tucker equations and convergence analysis of Newton and quasi-Newton methods for solving these equations,” Math. Oper. Res., vol. 22, pp. 301-325, 1997.
L. Qi and J. Sun, “A nonsmooth version of Newton's method,” Math. Prog., vol. 58, pp. 353-367, 1993.
L. Qi, D. Sun, and G. Zhou, “A new look at smoothing Newton methods for nonlinear complementarity problems and box constrained variational inequalities,” Math. Prog., vol. 87, pp. 1-35, 2000.
L. Qi and P. Tseng, “An analysis of piecewise smooth functions and almost smooth functions,” Department of Applied Mathematics, The Hong Kong Polytechnic University, Hong Kong, forthcoming.
D. Ralph and S. Scholtes, “Sensitivity analysis of composite piecewise smooth equations,” Math. Program., vol. 76, pp. 593-612, 1997.
R.T. Rockafellar, “Some properties of piecewise smooth functions,” Comput. Optim. Appl., vol. 25, pp. 247-250, 2003.
J.A. Roulier, “A convexity preserving grid refinement algorithm for interpolation of bivariate functions,” IEEE Comput. Graph. Appl., vol. 7, pp. 57-62, 1987.
J.W. Schmidt, “Rational biquadratic C 1-splines in S-convex interpolation,” Computing, vol. 47, pp. 87-96, 1991.
S. Scholtes, “Introduction to piecewise differentiable equations,” Habilitation Thesis, Preprint No. 54/1994, Institut für Statistik und Mathematische Wirtschaftstheorie, University of Karlsruhe, Karlsruhe, Germany, 1994.
D. Sun and L. Qi, “Solving variational inequality problems via smoothing-nonsmooth reformulations,” J. Comput. Appl. Math., vol. 129, pp. 37-62, 2001.
N. Yamashita and M. Fukushima, “Modified Newton methods for solving semismooth reformulations of monotone complementarity problems,” Math. Prog., vol. 76, pp. 469-491, 1997.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Qi, L., Yin, H. A Strongly Semismooth Integral Function and Its Application. Computational Optimization and Applications 25, 223–246 (2003). https://doi.org/10.1023/A:1022969507994
Issue Date:
DOI: https://doi.org/10.1023/A:1022969507994