Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Greenberg, Noam
Hirschfeldt, Denis R.
and
Nies, André
2012.
Characterizing the strongly jump-traceable sets via randomness.
Advances in Mathematics,
Vol. 231,
Issue. 3-4,
p.
2252.
Nies, André
2012.
Computably enumerable sets below random sets.
Annals of Pure and Applied Logic,
Vol. 163,
Issue. 11,
p.
1596.
Nies, André
2013.
Calibrating the complexity of $\Delta^{0}_{2}$ sets via their changes.
p.
285.




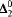 , 1-random set
, 1-random set 