Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-26T17:30:07.753Z Has data issue: false hasContentIssue false
  • English
  • Français

The non-compactness of square

Published online by Cambridge University Press:  12 March 2014

James Cummings ,
Matthew Foreman  and
Menachem Magidor
James Cummings
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh PA 15213, USA, E-mail: jcumming@andrew.cmu.edu
Matthew Foreman
Affiliation:
Department of Mathematics, University of California at Irvine, Irvine CA 92697, USA, E-mail: mforeman@math.uci.edu
Menachem Magidor
Affiliation:
Institute of Mathematics, Hebrew University of Jerusalem, Jerusalem 91904, Israel, E-mail: menachem@math.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Extract

This note proves two theorems. The first is that it is consistent to have 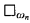for every n, but not have 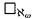. This is done by carefully collapsing a supercompact cardinal and adding square sequences to each ωn. The crux of the proof is that in the resulting model every stationary subset of ℵω+1 ⋂ cof(ω) reflects to an ordinal of cofinality ω1, that is to say it has stationary intersection with such an ordinal.

This result contrasts with compactness properties of square shown in [3]. In that paper it is shown that if one has square at every ωn, then there is a square type sequence on the points of cofinality ωk, k > 1 in ℵω+1. In particular at points of cofinality greater than ω1 there is a strongly non-reflecting stationary set of points of countable cofinality.

The second result answers a question of Džamonja, by showing that there can be no squarelike sequence above a supercompact cardinal, where “squarelike” means that one replaces the requirement that the cofinal sets be closed and unbounded by the requirement that they be stationary at all points of uncountable cofinality.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 68 , Issue 2 , June 2003 , pp. 637 - 643
Copyright
Copyright © Association for Symbolic Logic 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cummings, J., Collapsing successors of singulars, Proceedings of the American Mathematical Society, vol. 125 (1997), pp. 2703–2709.CrossRefGoogle Scholar
[2]Cummings, J., Foreman, M., and Magidor, M., Squares, scales and stationary reflection, Journal of Mathematical Logic, vol. 1 (2001), no. 1, pp. 35–99.CrossRefGoogle Scholar
[3]Cummings, J., Foreman, M., and Magidor, M., Canonical structure in the universe of set theory: Part I, to appear.Google Scholar
[4]Foreman, M., Games played on Boolean algebras, this Journal, vol. 48 (1983), pp. 714–723.Google Scholar
[5]Foreman, M. and Magidor, M., Mutually stationary sequences and the non-saturation of the non-stationary ideal on P κ(λ), Acta Mathematica, vol. 186 (2001), no. 2.CrossRefGoogle Scholar
[6]Laver, R., Making the supercompactness of κ indestructible under κ-directed closed forcing, Israel Journal of Mathematics, vol. 29 (1978), pp. 385–388.CrossRefGoogle Scholar
[7]Magidor, M., Foreman, M., and Shelah, S., Martin's maximum, saturated ideals and non-regular ultrafilters i, Annals of Mathematics, vol. 127 (1988), pp. 1–47.Google Scholar
[8]Namba, K., Independence proof of (ω, ω α)-distributive law in complete Boolean algebras, Commen-tarii Mathematici Universitatis Sancti Pauli, vol. 19 (1971), pp. 1–12.Google Scholar
[9]Namba, K., (ω 1, 2)-distributive law and perfect sets in generalized Baire space, Commentarii Mathematici Universitatis Sancti Pauli, vol. 20 (1971/1972), pp. 107–126.Google Scholar
[10]Shelah, S., Proper Forcing, North-Holland, Amsterdam, 1980.Google Scholar