Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-24T15:24:18.060Z Has data issue: false hasContentIssue false
  • English
  • Français

A structure theorem for strongly abelian varieties with few models

Published online by Cambridge University Press:  12 March 2014

Bradd Hart  and
Matthew Valeriote
Bradd Hart
Affiliation:
Department of Mathematics, University of California, Berkeley, California 94720 Department of Mathematics, Mcmaster University, Hamilton, Ontario L8S 4K1, Canada
Matthew Valeriote
Affiliation:
Department of Mathematics, Mcmaster University, Hamilton, Ontario L8S 4K1, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

By a variety, we mean a class of structures in some language 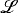containing only function symbols which is equationally defined or equivalently is closed under homomorphisms, submodels and products.

If K is a class of 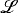-structures then I(K, λ) denotes the number of nonisomorphic models in K of cardinality λ. When we say that K has few models, we mean that I(K,λ) < 2λ for some λ > ∣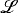∣. If I(K,λ) = 2λ for all λ > ∣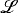∣, then we say K has many models. In [9] and [10], Shelah has shown that for an elementary class K, having few models is a strong structural condition.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 3 , September 1991 , pp. 832 - 852
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Baldwin, J. and Mckenzie, R., Counting models in universal Horn classes, Algebra Universalis, vol. 15 (1982), pp. 359–384.CrossRefGoogle Scholar
[2] Baldwin, John T., Fundamentals of stability theory, Springer-Verlag, Berlin, 1988.CrossRefGoogle Scholar
[3] Harrington, Leo and Makkai, Michael, The main gap: Counting uncountable models of ω-stable and superstable theories, Notre Dame Journal of Formal Logic, vol. 26 (1985), pp. 139–177.CrossRefGoogle Scholar
[4] McKenzie, R. and Valeriote, M., The structure of locally finite decidable varieties, Birkhäuser, Basel, 1989.CrossRefGoogle Scholar
[5] Palyutin, E. A., Spectra of varieties, Doklady AkademiiNauk SSSR, vol. 306 (1989), pp. 789–790; English translation, Soviet Mathematics Doklady, vol. 39 (1989), pp. 553-554.Google Scholar
[6] Palyutin, E. A. and Starchenko, S. S., Spectra of Horn classes, Doklady Akademii Nauk SSSR, vol. 290 (1986), pp. 1298–1300; English translation, Soviet Mathematics Doklady , vol. 34 (1987), pp. 394–396.Google Scholar
[7] Saffe, J., Palyutin, E. and Starchenko, S., Models of superstable Horn theories, Algebra i Logika, vol. 24 (1985), pp. 278–326; English translation, Algebra and Logic , vol. 24 (1985), pp. 171–209.Google Scholar
[8] Prest, M., Model theory and modules, Cambridge University Press, Cambridge, 1988.CrossRefGoogle Scholar
[9] Shelah, S., Classification theory and the number of non-isomorphic models, North-Holland, Amsterdam, 1978.Google Scholar
[10] Shelah, S., The spectrum problem. 4: The main gap for countable theories, to be included in the forthcoming revised edition of [9].Google Scholar
[11] Valeriote, M., On decidable locally finite varieties, Ph.D. thesis, University of California, Berkeley, California, 1986.Google Scholar