Article contents
Simplicial structures in MV-algebras and logic
Published online by Cambridge University Press: 12 March 2014
Extract
Classical logic, as is well known, can be analyzed in a great part by algebraic methods using the Lindenbaum algebra obtained from the formal system. For example the completeness theorem for this logic becomes equivalent to the semisimplicity of the obtained Lindenbaum algebra.
Since Chang [4, 5], Łukasiewicz logic has also been analyzed algebraically through the associated Lindenbaum type algebra, that is the algebra of equivalence classes obtained from the relation of provable equivalence. In this case this algebra is an MV-algebra [4]. Once again logical notions have an algebraic counterpart, for example, completeness relates strongly to semisimplicity [4, 5]. However, unlike the classical case where the algebras in question are Boolean and always semisimple, not all MV-algebras are semisimple. This fact, in a sense, enriches the theory of MV-algebras.
Now every MV-algebra can be considered a Lindenbaum type algebra, namely an algebra associated to Łukasiewicz logic with additional axioms. Thus we can carry over to any MV-algebra various logical notions such as (in) completeness, consistency, satisfiability, etc.
Two important logical notions are those of “formal consequence” and “semantical consequence”. The former just says that a wff α is deducible from a set of wff 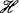 via the axioms and rules of inference, while the latter just says that every evaluation that “satisfies” all the members of
via the axioms and rules of inference, while the latter just says that every evaluation that “satisfies” all the members of 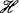 also “satisfies” α.
also “satisfies” α.
Informally call these relations F, S respectively; consider them as binary relations, 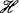 Fα and
Fα and 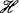 Sα.
Sα.
Now the completeness theorem just states F = S. Thus we can talk about an MV-algebra being “complete” provided the associated relations F, S are equal.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2007
References
REFERENCES
- 2
- Cited by




