No CrossRef data available.
Article contents
Congruence relations on lattices of recursively enumerable sets
Published online by Cambridge University Press: 12 March 2014
Extract
Let {We}e∈ω be a standard enumeration of the recursively enumerable (r. e.) subsets of ω = {0, 1, 2, …}. The lattice of recursively enumerable sets, 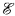 is the structure ({We}e∈ω, ∪, ∩).
is the structure ({We}e∈ω, ∪, ∩). 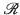 is the sublattice of
is the sublattice of 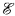 consisting of the recursive sets.
consisting of the recursive sets.
Suppose 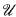 is a lattice of subsets of ω. ≡ is said to be a congruence relation on
is a lattice of subsets of ω. ≡ is said to be a congruence relation on 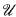 if ≡ is an equivalence relation on
if ≡ is an equivalence relation on 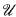 and if for all U, U′ ∈
and if for all U, U′ ∈ 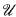 and V, V ∈
and V, V ∈ 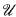 , if U ≡ U′ and V ≡ V′ then U ∪ U′ ≡ V ∪ V′ and U ∩ U′ ≡ V ∩ V′. [U] = {V ∈
, if U ≡ U′ and V ≡ V′ then U ∪ U′ ≡ V ∪ V′ and U ∩ U′ ≡ V ∩ V′. [U] = {V ∈ 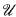 | V ≡ U} is the equivalence class of U. If ≡ is a congruence relation on
| V ≡ U} is the equivalence class of U. If ≡ is a congruence relation on 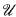 , the elements of the quotient lattice
, the elements of the quotient lattice 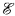 / ≡ are the equivalence classes of ≡. [U] ∪ [V] is defined as [U ∪ V], and [U] ∩ [V] is defined as [U ∩ V].
/ ≡ are the equivalence classes of ≡. [U] ∪ [V] is defined as [U ∪ V], and [U] ∩ [V] is defined as [U ∩ V].
The quotient lattices of 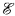 (or of some sublattice
(or of some sublattice 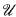 ) correspond naturally with the congruence relations which give rise to them, and in turn the congruence relations of sublattices of
) correspond naturally with the congruence relations which give rise to them, and in turn the congruence relations of sublattices of 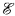 can be characterized in part by their computational complexity. The aim of the present paper is to characterize congruence relations in some of the most important complexity classes.
can be characterized in part by their computational complexity. The aim of the present paper is to characterize congruence relations in some of the most important complexity classes.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2002




