Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T18:11:18.027Z Has data issue: false hasContentIssue false
  • English
  • Français

Some results in polychromatic Ramsey theory

Published online by Cambridge University Press:  12 March 2014

Uri Abraham ,
James Cummings  and
Clifford Smyth
Uri Abraham
Affiliation:
Mathematics and Computer Science Department, Ben-Gurion University, Beer-Sheva, 84105, Israel. E-mail: abraham@math.bgu.ac.il
James Cummings
Affiliation:
Mathematical Sciences Department, Carnegie Mellon University, Pittsburgh PA 15215, USA. E-mail: jcumming@andrew.cmu.edu
Clifford Smyth
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge MA 02139, USA. E-mail: csmyth@math.mit.edu
Get access Rights & Permissions [Opens in a new window]

Extract

Classical Ramsey theory (at least in its simplest form) is concerned with problems of the following kind: given a set X and a colouring of the set [X]n of unordered n-tuples from X, find a subset Y ⊆ X such that all elements of [Y]n get the same colour. Subsets with this property are called monochromatic or homogeneous, and a typical positive result in Ramsey theory has the form that when X is large enough and the number of colours is small enough we can expect to find reasonably large monochromatic sets.

Polychromatic Ramsey theory is concerned with a “dual” problem, in which we are given a colouring of [X]n and are looking for subsets Y ⊆ X such that any two distinct elements of [Y]n get different colours. Subsets with this property are called polychromatic or rainbow. Naturally if we are looking for rainbow subsets then our task becomes easier when there are many colours. In particular given an integer k we say that a colouring is k-bounded when each colour is used for at most k many n-tuples.

At this point it will be convenient to introduce a compact notation for stating results in polychromatic Ramsey theory. We recall that in classical Ramsey theory we write 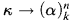to mean “every colouring of [κ]n in k colours has a monochromatic set of order type α”. We will write 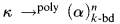to mean “every k-bounded colouring of [κ]n has a polychromatic set of order type α”. We note that when κ is infinite and k is finite a k-bounded colouring will use exactly κ colours, so we may as well assume that κ is the set of colours used.

Keywords

Polychromatic Ramsey theoryforcing axioms
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 3 , September 2007 , pp. 865 - 896
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Abraham, U., Proper forcing, To appear in the handbook of set theory.Google Scholar
[2] Abraham, U. and Todorčević, S., Martin's axiom and first-countable S- and L-spaces, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J.E., editors), North-Holland, Amsterdam, 1984, pp. 327–346.Google Scholar
[3] Alspach, B., Gerson, M., Hahn, G., and Hell, P., On sub-Ramsey numbers, Ars Combinatoria, vol. 22 (1986), pp. 199–206.Google Scholar
[4] Baumgartner, J. and Hajnal, A., A proof (involving Martin's axiom) of a partition relation. Fundamentu Mathematicae, vol. 78 (1973), no. 3, pp. 193–203.Google Scholar
[5] Baumgartner, J. E., Applications of the proper forcing axiom, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J.E., editors), North-Holland, Amsterdam, 1984, pp. 913–959.Google Scholar
[6] Beaudoin, Robert E., The proper forcing axiom and stationary set reflection, Pucific Journal of Mathematics, vol. 149 (1991), no. 1, pp. 13–24.Google Scholar
[7] Erdős, P., Nešetřil, J., and Rödl, V., On some problems related to partitions of edges of a graph, Graphs and other combinatorial topics (Prague, 1982), Teubner-Texte Mathematik, vol. 59, Teubner, Leipzig, 1983, pp. 54–63.Google Scholar
[8] Foreman, M., Games played on Boolean algebras, this Journal, vol. 48 (1983), no. 3, pp. 714–723.Google Scholar
[9] Foreman, M., Magidor, M., and Shelah, S., Martin's maximum, saturated ideals, and nonregular ultrafilters. I, Annals of Mathematics. Second Series, vol. 127 (1988), no. 1, pp. 1–47.Google Scholar
[10] Galvin, F., Advanced problem number 6034, The American Mathematical Monthly, vol. 82 (1975), p. 529.Google Scholar
[11] Galvin, F., Letters to S. Todorcevic, cited in [17].Google Scholar
[12] Hell, P. and Montellano-Ballesteros, J. J., Polychromatic cliques, Discrete Mathematics, vol. 285 (2004), no. 1-3, pp. 319–322.CrossRefGoogle Scholar
[13] Prömel, H. J. and Voigt, B., Canonical forms of Borel-measurable mappings ∆: [ω]ω → R, Journal of Combinatorial Theory. Series A, vol. 40 (1985), no. 2, pp. 409–417.CrossRefGoogle Scholar
[14] Schipperus, R., The topological Baumgartner-Hajnal theorem, To appear.Google Scholar
[15] Shelah, S., Proper and improper forcing, second ed., Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998.CrossRefGoogle Scholar
[16] Soukup, L., Indestructible properties of S- and L-spaces, Topology and its Applications, vol. 112 (2001), no. 3, pp. 245–257.CrossRefGoogle Scholar
[17] Todorčević, Stevo, Forcing positive partition relations. Transactions of the American Mathematical Society, vol. 280 (1983), no. 2, pp. 703–720.CrossRefGoogle Scholar
[18] Todorčević, Stevo, A note on the proper forcing axiom, Axiomatic set theory (Boulder, Colorado, 1983), Contemporary Mathematics, vol. 31, American Mathematical Society, Providence, RI, 1984, pp. 209–218.Google Scholar
[19] Todorčević, Stevo, Partitioning pairs of countable ordinals, Acta Mathematica, vol. 159 (1987), no. 3-4, pp. 261–294.CrossRefGoogle Scholar