Article contents
On completely recursively enumerable classes and their key arrays1
Published online by Cambridge University Press: 12 March 2014
Extract
The two results of this paper (a theorem and an example) are applications of a device described in section 1. Our notation is that of [4], with which we assume familiarity. It may be worth while to mention in particular the function Φ(n, x) which recursively enumerates the partial recursive functions of one variable, the Cantor enumerating functions J(x, y), K(x), L(x), and the classes F and Q of r.e. (recursively enumerable) and finite sets respectively.
It is possible to “give” a finite set in a way which conveys the maximum amount of information; this may be called “giving explicitly”, and it requires that in addition to an effective enumeration or decision procedure for the set we give its cardinal number. It is sometimes desired to enumerate effectively an infinite class of finite sets, each given explicitly (e.g., [4] p. 360, or Dekker [1] p. 497), and we suggest here a device for doing this.
We set up an effective one-to-one correspondence between the finite sets of non-negative integers and these integers themselves: the integer 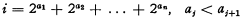 , corresponds to the set αi, = {a1, a2, …, an} and inversely. α0 is the empty set. Clearly i can be effectively computed from the elements of αi and its cardinal number.
, corresponds to the set αi, = {a1, a2, …, an} and inversely. α0 is the empty set. Clearly i can be effectively computed from the elements of αi and its cardinal number.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1956
Footnotes
The work reported in this paper was supported by the National Science Foundation.
References
REFERENCES
- 42
- Cited by




