Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-26T18:29:00.262Z Has data issue: false hasContentIssue false
  • English
  • Français

A lattice of interpretability types of theories1

Published online by Cambridge University Press:  12 March 2014

Jan Mycielski
Jan Mycielski*
Affiliation:
University of Colorado, Boulder, Colorado 80309
Get access Rights & Permissions [Opens in a new window]

Extract

We consider first-order logic only. A theory S will be called locally interpretable in a theory T if every theorem of S is interpretable in T. If S is locally interpretable in T and T is consistent then S is consistent. Most known relative consistency proofs can be viewed as local interpretations. The classic examples are the cartesian interpretation of the elementary theorems of Euclidean n-dimensional geometry into the first-order theory of real closed fields, the interpretation of the arithmetic of integers (rational numbers) into the arithmetic of positive integers, the interpretation of ZF + (V = L) into ZF, the interpretation of analysis into ZFC, relative consistency proofs by forcing, etc. Those interpretations are global. Under fairly general conditions local interpretability implies global interpretability; see Remarks (7), (8), and (9) below.

We define the type (interpretability type) of a theory S to be the class of all theories T such that S is locally interpretable in T and vice versa. There happen to be 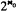such types and they are partially ordered by the relation of local interpretability. This partial ordering is of lattice type and has the following form:

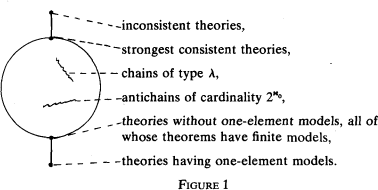
The lattice is distributive and complete and satisfies the infinite distributivity law of Brouwerian lattices:

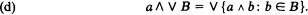
We do not know if the dual law

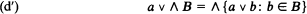
is true. We will show that the lattice is algebraic and that its compact elements form a sublattice and are precisely the types of finitely axiomatizable theories, and several other facts.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 42 , Issue 2 , June 1977 , pp. 297 - 305
Copyright
Copyright © Association for Symbolic Logic 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Work supported by NSF grant GP–43786.

References

REFERENCES

[1]Balbes, R. and Dwinger, Ph., Distributive lattices, University of Missouri Press, 1975.Google Scholar
[2]Feferman, S., Arithmetization of metamathematics in a general setting, Fundamenta Mathematicae, vol. 49 (1960), pp. 35–92.CrossRefGoogle Scholar
[3]Grätzer, George, Lattice theory, first concepts and distributive lattices, Freeman and Company, San Francisco, 1971.Google Scholar
[4]Jeroslow, R. G., Consistency statements in formal theories, Fundamenta Mathematicae, vol. 72 (1971), pp. 17–40.CrossRefGoogle Scholar
[5]McKenzie, Ralph, On spectra and the negative solution of the decision problem for identities having a finite nontrivial model, this Journal, vol. 40 (1975), pp. 186–196.Google Scholar
[6]Montague, R., Theories incomparable with respect to relative interpretability, this Journal, vol. 27 (1962), pp. 195–211.Google Scholar
[7]Montague, R. and Vaught, R. L., A note on theories with selectors, Fundamenta Mathematicae, vol. 47 (1959), pp. 243–247.Google Scholar
[8]Mycielski, J., A lattice connected with relative interpretability of theories, Notices of the American Mathematical Society, vol. 9 (1962), pp. 407–408; errata, J. Mycielski, A lattice connected with relative interpretability of theories, Notices of the American Mathematical Society, vol. 18 (1971), p. 984.Google Scholar
[9]Neumann, W. D., On Malcev conditions, Journal of the Australian Mathematical Society, vol. 17 (1974), pp. 376–384.Google Scholar
[10]Orey, Steven, Relative interpretations, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 7 (1961), pp. 146–153.CrossRefGoogle Scholar
[11]Szczerba, L., Interpretability of elementary theories, Proceedings of the 5th International Congress for Logic, Philosophy and Methodology of Science.Google Scholar
[12]Tarski, A., What is elementary geometry? Symposium on the axiomatic method, with special reference to geometry and physics, Amsterdam, 1959, pp. 16–29.Google Scholar
[13]Vaught, R. L., On a theorem of Cobham concerning undecidable theories, Logic, methodology and philosophy of science, Proceedings of the 1960 International Congress (Nagel, E., Suppes, P. and Tarski, A., Editors), Stanford, California, 1962, pp. 14–25.Google Scholar
[14]Vaught, R. L., Axiomatizability by a schema, this Journal, vol. 32 (1967), pp. 473–479.Google Scholar