Article contents
Sets constructible from sequences of ultrafilters
Published online by Cambridge University Press: 12 March 2014
Extract
In [4], Kunen used iterated ultrapowers to show that if U is a normal κ-complete nontrivial ultrafilter on a cardinal κ then L[U], the class of sets constructive from U, has only the ultrafilter U ∩ L[U] and this ultrafilter depends only on κ. In this paper we extend Kunen's methods to arbitrary sequences U of ultrafilters (provided that they fulfill a coherency condition) and obtain generalizations of these results (§3). In particular we answer Problem 1 of Kunen and Paris [5] which asks whether the number of ultrafilters on κ can be intermediate between 1 and 22κ. If there is a normal κ-complete ultrafilter U on κ such that {α < κ: α is measurable} ∈ U then there is an inner model with exactly two normal ultrafilters on κ, and if κ is super-compact then there are inner models having κ+ +, κ+ or any cardinal less than or equal to κ normal ultrafilters (§4).
These methods also show that several properties of L which had been shown to hold for L[U] also hold for L[U]: using an idea of Silver we show that in L[U] the generalized continuum hypothesis is true, there is a Souslin tree, and there is a 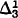 well-ordering of the reals. In addition we generalize a result of Kunen to characterize the countaby complete ultrafilters of L[U].
well-ordering of the reals. In addition we generalize a result of Kunen to characterize the countaby complete ultrafilters of L[U].
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
References
REFERENCES
- 62
- Cited by




