Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T16:11:36.037Z Has data issue: false hasContentIssue false
  • English
  • Français

On n-quantifier induction

Published online by Cambridge University Press:  12 March 2014

Charles Parsons
Charles Parsons*
Affiliation:
Columbia University, New York, New York 10027
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we discuss subsystems of number theory based on restrictions on induction in terms of quantifiers, and we show that all the natural formulations of ‘n-quantifier induction’ are reducible to one of two (for n ≠ 0) nonequivalent normal forms: the axiom of induction restricted to 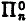(or, equivalently, 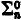) formulae and the rule of induction restricted to 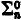formulae.

Let Z0 be classical elementary number theory with a symbol and defining equations for each Kalmar elementary function, and the rule of induction

restricted to quantifier-free formulae. Given the schema

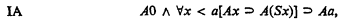
let IAn be the restriction of IA to formulae of Z0 with ≤n nested quantifiers, IAn′ to formulae with ≤n nested quantifiers, disregarding bounded quantifiers, 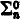the restriction to 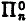formulae, 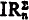the restriction to 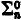, formulae. IRn, IRn′, 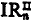, 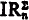are analogous.

Then, we show that, for every n, 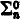, , 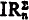IAn, and IAn′, are all equivalent modulo Z0. The corresponding statement does not hold for IR. We show that, if n ≠ 0, 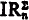is reducible to 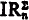; evidently IRn is reducible to 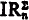. On the other hand, IRn′ is obviously equivalent to IAn′ [10, Lemma 2].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 37 , Issue 3 , September 1972 , pp. 466 - 482
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Diller, Justus and Schütte, Kurt, Simultane Rekursionen in der Theorie der Funktionale endlicher Typen, Archiv für mathematische Logik und Grundlagenforschung, vol. 14 (1971), pp. 69–74.CrossRefGoogle Scholar
[2]Dreben, Burton and Denton, John, Herbrand-style consistency proofs, in Intuitionism and proof theory, North-Holland, Amsterdam, 1970, pp. 419–434.Google Scholar
[3]Howard, W. A., Functional interpretation of bar induction by bar recursion, Compositio Mathematica, vol. 20 (1968), pp. 107–124.Google Scholar
[4]Kleene, S. C., Introduction to metamathematics, Van Nostrand, New York, 1952.Google Scholar
[5]Kreisel, G., On the concepts of completeness and interpretation of formal systems, Fundamenta Mathematicae, vol. 39 (1952), pp. 103–127.CrossRefGoogle Scholar
[6]Kreisel, G., Interpretation of analysis by constructive functionals of finite types, Constructivity in mathematics (Heyting, A., ed.), North-Holland, Amsterdam, 1959, pp. 101–129.Google Scholar
[7]Kreisel, G., Inessential extensions of Heyting's arithmetic by means of functionals of finite type, this Journal, vol. 24 (1959), p. 284 (Abstract).Google Scholar
[8]Kreisel, G., A survey of proof theory, this Journal, vol. 33 (1968), pp. 321–384.Google Scholar
[9]Kreisel, G., Lacombe, D. and Shoenfield, J. R., Effective operations and partial recursive functionals, Constructivity in mathematics (Heyting, A., ed.), North-Holland, Amsterdam, 1959, pp. 290–297.Google Scholar
[10]Parsons, Charles, On a number-theoretic choice schema and its relation to induction, Intuitionism and proof theory, North-Holland, Amsterdam, 1970, pp. 459–473.Google Scholar
[11]Spector, Clifford, Provably recursive functionals of analysis, Proceedings of Symposia in Pure Mathematics, Vol. 5, 1962, pp. 1–27.CrossRefGoogle Scholar
[12]Tait, W. W., Nested recursion, Mathematische Annalen, vol. 143 (1961), pp. 236–250.CrossRefGoogle Scholar
[13]Tait, W. W., Intensional interpretations of functionals of finite type. I, this Journal, vol. 32 (1967), pp. 197–215.Google Scholar
[14]Tait, W. W., Constructive reasoning, Logic, methodology, and philosophy of science. III (Rootselaar, B. van and Staal, J. F., Editors), North-Holland, Amsterdam, 1968, pp. 185–198.CrossRefGoogle Scholar
[15]Parsons, Charles, Proof-theoretic analysis of restricted induction schemata, this Journal vol. 36 (1971), p. 361 (Abstract).Google Scholar
[16]Parsons, Charles, On a number-theoretic choice schema. II, this Journal, vol. 36 (1971), p. 587 (Abstract).Google Scholar