Ackermann's set theory A* is usually formulated in the first order predicate calculus with identity, ∈ for membership and V, an individual constant, for the class of all sets. We use small Greek letters to represent formulae which do not contain V and large Greek letters to represent any formulae. The axioms of A* are the universal closures of

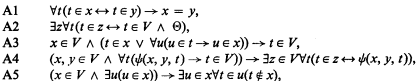
where all free variables are shown in A4 and z does not occur in the Θ of A2.

A+ is a generalisation of A* which Reinhardt introduced in [3] as an attempt to provide an elaboration of Ackermann's idea of “sharply delimited” collections. The language of A+ is that of A*'s augmented by a new constant V′, and its axioms are A1–A3, A5, V ⊆ V′ and the universal closure of

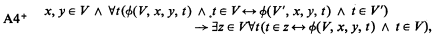
where all free variables are shown.

Using a schema of indescribability, Reinhardt states in [3] that if ZF + ‘there exists a measurable cardinal’ is consistent then so is A+, and using [4] this result can be improved to a weaker large cardinal axiom. It seemed plausible that A+ was stronger than ZF, but our main result, which is contained in Theorem 5, shows that if ZF is consistent then so is A+, giving an improvement on the above results.