Article contents
Uncountable models and infinitary elementary extensions
Published online by Cambridge University Press: 12 March 2014
Extract
Let A be a countable admissible set (as defined in [1], [3]). The language LA consists of all infinitary finite-quantifier formulas (identified with sets, as in [1]) that are elements of A. Notationally, LA = A ∩ Lω1ω. Then LA is a countable subset of Lω1ω, the language of all infinitary finite-quantifier formulas with all conjunctions countable. The set 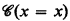 is the set of Lω1ω sentences defined in 2.2 below. The following theorem characterizes those A-Σ1 sets Φ of LA sentences that have uncountable models.
is the set of Lω1ω sentences defined in 2.2 below. The following theorem characterizes those A-Σ1 sets Φ of LA sentences that have uncountable models.
Main Theorem (3.1.). If Φ is an A-Σ1set of LA sentences, then the following are equivalent:
(a) Φ has an uncountable model,
(b) Φ has a model with a proper LA-elementary extension,
(c) for every 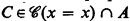 , ⋀Φ → C is not valid.
, ⋀Φ → C is not valid.
This theorem was announced in [2] and is proved in §§3, 4, 5. Makkai's earlier [4, Theorem 1] implies that, if Φ determines countable structure 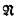 up to Lω1ω-elementary equivalence, then (a) is equivalent to (c′) for all
up to Lω1ω-elementary equivalence, then (a) is equivalent to (c′) for all 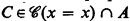 , ⋀Φ → C is not valid.
, ⋀Φ → C is not valid.
The requirement in 3.1 that Φ is A-Σ1 is essential when the set ω of all natural numbers is an element of A. For by the example of [2], then there is a set Φ LA sentences such that (b) holds and (a) fails; it is easier to show that, if ω ϵ A, there is a set Φ of LA sentences such that (c) holds and (b) fails.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1973
References
REFERENCES
- 6
- Cited by




