The central notion of this paper is that of a (conjunctive) game-sentence, i.e., a sentence of the form

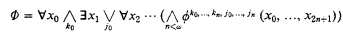
where the indices ki, ji range over given countable sets and the matrix conjuncts are, say, open -formulas. Such game sentences were first considered, independently, by Svenonius [19], Moschovakis [13]—[15] and Vaught [20]. Other references are [1], [3]—[5], [10]—[12]. The following normal form theorem was proved by Vaught (and, in less general forms, by his predecessors).

Theorem 0.1. Let L = L0(R). For every -sentence ϕ there is an L0-game sentence Θ such that ⊨′ ∃Rϕ ↔ Θ.

(A word about the notations: L0(R) denotes the language obtained from L0 by adding to it the sequence R of logical symbols which do not belong to L0; “⊨′α” means that α is true in all countable models.)

0.1 can be restated as follows.

Theorem 0.1′. For every-sentence ϕ there is an L0-game sentence Θ such that ⊨ϕ → Θ and for any-sentence ϕ if ⊨ϕ → ϕ and L′ ⋂ L ⊆ L0, then ⊨ Θ → ϕ.

(We sketch the proof of the equivalence between 0.1 and 0.1′.

0.1 implies 0.1′. This is obvious once we realize that game sentences and their negations satisfy the downward Löwenheim-Skolem theorem and hence, ⊨′α is equivalent to ⊨α whenever α is a boolean combination of and game sentences.