Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-25T00:57:33.740Z Has data issue: false hasContentIssue false
  • English
  • Français

A combinatorial property of the homomorphism relation between countable order types

Published online by Cambridge University Press:  12 March 2014

Charles Landraitis
Charles Landraitis*
Affiliation:
Boston College, Chestnut Hill, Massachusetts 02115
Get access Rights & Permissions [Opens in a new window]

Extract

The relation ≪ (is a homomorphic image of) between (linear) order types has properties similar to those of the better known relation ≤ (is embeddable in). For example, the order type η of the rationals not only embeds every countable order type 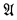but also maps homomorphically onto 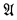. If 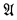is scattered, then 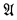can be embedded in (ω* + ω)α for some α < ω1. In that case, 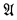is also a homomorphic image of (ω* + ω)α [Lan 2]. If 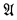is uncountable, then for some uncountable ordinal α, α ≪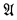, α* ≪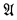, or η ≪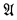. Proofs of these facts are much the same for ≤ and ≪.

The main theorem of [Lav 1] implies that the embedding relation better-quasiorders the set of countable order types. Our main theorem (§3) states the analogous result for the homomorphism relation. As a consequence, if 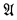0, 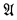1, … is an infinite sequence of countable order types, then there are i, j, i < j, such that 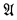i, is a homomorphic image of 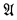j. We observed in [Lan 1] that if this is true, then for each countable order type 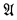there is a sentence 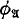of Lω1ω such that if 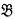is a countable order type, then 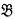satisfies 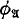if and only if 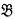is a homomorphic image of 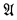. In fact, the motivation for the work leading to this paper came from this observation.

On the negative side, it is pointed out (§3) that our theorem cannot be extended as far as that of [Lav 1].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 44 , Issue 3 , September 1979 , pp. 403 - 411
Copyright
Copyright © Association for Symbolic Logic 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

[Ha]Hausdorff, F., Grundzüge einer théorie der geordneten mengen, Mathematische Annalen, vol. 65(1908), pp. 435–505.CrossRefGoogle Scholar
[Lan 1]Landraitis, C., Definability in well quasi-ordered sets of structures, this Journal, vol. 42(1977), pp. 289–291.Google Scholar
[Lan 2]Landraitis, C., Ph. D. dissertation, Dartmouth College, 1975.Google Scholar
[Lav 1]Laver, R., On Fraisses' order type conjecture, Annals of Mathematics, vol. 93(1971), pp. 89–111.CrossRefGoogle Scholar
[Lav 2]Laver, R., Better-quasi-orderings and a class of trees, Studies in foundations and combinatorics, Academic Press, 1978.Google Scholar
[NW 1]Nash-Williams, C. St. J. A., On well-quasi-ordering transfinite sequences, Proceedings of the Cambridge Philosophical Society, vol. 61(1965), pp. 33–39.CrossRefGoogle Scholar
[NW 2]Laver, R., On well quasi-ordering infinite trees, Proceedings of the Cambridge Philosophical Society, vol. 61(1965), pp. 697–720.Google Scholar
[R]Rosenstein, J. G., Linear orderings (to appear).Google Scholar
[S]Sierpinski, W., Cardinal and ordinal numbers, 2nd edition, Panstwowe Wydawnictwo Naukowe, Polish Scientific Publications, Warsaw, 1965.Google Scholar