Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-24T03:24:03.063Z Has data issue: false hasContentIssue false
  • English
  • Français

The lattice of modal logics: an algebraic investigation

Published online by Cambridge University Press:  12 March 2014

W. J. Blok
W. J. Blok*
Affiliation:
Mathematisch Instituut, Universiteit van Amsterdam
Get access Rights & Permissions [Opens in a new window]

Abstract

Modal logics are studied in their algebraic disguise of varieties of so-called modal algebras. This enables us to apply strong results of a universal algebraic nature, notably those obtained by B. Jónsson. It is shown that the degree of incompleteness with respect to Kripke semantics of any modal logic containing the axiom □p→P or containing an axiom of the form □mp↔□m+1p for some natural number m is . 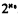Furthermore, we show that there exists an immediate predecessor of classical logic (axiomatized by p↔□p) which is not characterized by any finite algebra. The existence of modal logics having 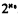immediate predecessors is established. In contrast with these results we prove that the lattice of extensions of S4 behaves much better: a logic extending S4 is characterized by a finite algebra iff it has finitely many extensions and any such logic has only finitely many immediate predecessors, all of which are characterized by a finite algebra.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 45 , Issue 2 , June 1980 , pp. 221 - 236
Copyright
Copyright © Association for Symbolic Logic 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Blok, W. J., The lattice of modal logics is not strongly atomic, Algebra Universalis (to appear).Google Scholar
[2]Blok, W. J., Varieties of interior algebras, dissertation, University of Amsterdam, 1976.Google Scholar
[3]Blok, W. J. and Dwinger, Ph., Equational classes of closure algebras. I, Indagatlones Mathematical, vol. 37 (1975), pp. 189–198.CrossRefGoogle Scholar
[4]Fine, K., An incomplete logic containing S4, Theoria, vol. 40 (1974), pp. 23–29.CrossRefGoogle Scholar
[5]Grätzer, G., Universal algebra. Van Nostrand, Princeton, NJ, 1968.Google Scholar
[6]Jónsson, B., Algebras whose congruence lattices are distributive, Mathematica Seandinavica, vol. 21 (1967), pp. 110–121.CrossRefGoogle Scholar
[7]Lemmon, E. J., Algebraic semantics for modal logics. I, this Journal, vol. 31 (1966), pp. 46–65.Google Scholar
[8]Makinson, D. C., Some embedding theorems for modal logic, Notre Dame Journal of Formal Logic, vol. 12 (1971), pp. 252–254.CrossRefGoogle Scholar
[9]Thomason, S. K., An incompleteness theorem in modal logic, Theoria, vol. 40 (1974), pp. 30–34.CrossRefGoogle Scholar
[10]Thomason, S. K., Semantic analysis of tense logics, this Journal, vol. 37 (1972), pp. 150–158.Google Scholar