In [6], G. Metakides and the author introduced a general model theoretic setting in which to study the lattice of r.e. substructures of a large class of recursively presented models 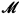. Examples included 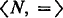, the natural numbers with equality, 〈 Q, ≤ 〉, the rationals under the usual ordering, and a large class of n-dimensional partial orderings. In this setting, we were able to generalize many of the constructions of classical recursion theory so that the constructions yield the classical results when we specialize to the case of 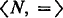and new results when we specialize to other models. Constructions to generalize Myhill's Theorem on creative sets [8], Friedberg's Theorem on the existence of maximal sets [3], Dekker's Theorem on the degrees of hypersimple sets [2], and Martin's Theorem on the degrees of maximal sets [5] were produced in [6]. In this paper, we give constructions to generalize the Morley-Soare Splitting Theorem [7] and Lachlan's characterization of hyperhypersimple sets [4] in §2, constructions to generalize Lachlan's theorems on the existence of major subsets and r-maximal sets contained in maximal sets [4] in §3, and constructions to generalize Robinson's construction of r-maximal sets that are not contained in any maximal sets [11] and second-order maximal sets [12] in §4.

In §1 of this paper, we give the precise definitions of our model theoretic setting and deal with other preliminaries. Also in §1, we define the notions of “uniformly nonrecursive”, “uniformly maximal”, etc. which are the key notions involved in the generalizations of the various theorems that occur in §§2, 3 and 4.