Article contents
Dimension theory and homogeneity for elementary extensions of a model
Published online by Cambridge University Press: 12 March 2014
Extract
We take a fixed countable model M0, and we look at the structure of and number of its countable elementary extensions (up to isomorphism over M0). Assuming that S(M0) is countable, we prove that if N is a weakly minimal extension of 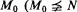 , and if
, and if 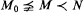 then there is an elementary embedding of N into M over M0), then N is homogeneous over M0. Moreover the condition that ∣S(M0)∣ = ℵ0 cannot be removed. Under the hypothesis that M0 contains no infinite set of tuples ordered by a formula, we prove that M0 has infinitely many countable elementary extensions up to isomorphism over M0. A preliminary result is that all types over M0 are definable, and moreover
then there is an elementary embedding of N into M over M0), then N is homogeneous over M0. Moreover the condition that ∣S(M0)∣ = ℵ0 cannot be removed. Under the hypothesis that M0 contains no infinite set of tuples ordered by a formula, we prove that M0 has infinitely many countable elementary extensions up to isomorphism over M0. A preliminary result is that all types over M0 are definable, and moreover  is definable over M0 if and only if
is definable over M0 if and only if 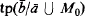 is definable over M0 (forking symmetry). We also introduce a notion of relative homogeneity, and show that a large class of elementary extensions of M0 are relatively homogeneous over M0 (under the assumptions that M0 has no order and S(M0) is countable).
is definable over M0 (forking symmetry). We also introduce a notion of relative homogeneity, and show that a large class of elementary extensions of M0 are relatively homogeneous over M0 (under the assumptions that M0 has no order and S(M0) is countable).
I will now discuss the background to and motivation behind the results in this paper, and also the place of this paper relative to other conjectures and investigations. To simplify notation let T denote the complete diagram of M0. First, our result that if M0 has no order then T has infinitely many countable models is related to the following conjecture: any theory with a finite number (more than one) of countable models is unstable.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1982
References
REFERENCES
- 5
- Cited by




