Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-24T09:03:20.740Z Has data issue: false hasContentIssue false
  • English
  • Français

The generalised RK-order, orthogonality and regular types for modules

Published online by Cambridge University Press:  12 March 2014

Mike Prest
Mike Prest*
Affiliation:
Mathematics Department, Yale University, New Haven, Connecticut 06520
*
Department of Pure Mathematics, University of Liverpool, Liverpool L69 3BX, England
Get access Rights & Permissions [Opens in a new window]

Extract

I characterise various model-theoretic properties of types, in complete theories of modules, in terms of the algebraic structure of pure-injective modules. More specifically, I consider the generalised RK-order, and the relation of domination between types, orthogonality of types, and regular types. It will be seen that, essentially, it is the stationary types over pure-injective models which bear the algebraic structural information.

For background in the model theory of modules, see [4], [5], [13], [17], [19], and for the model-theoretic background [10], [11], [12], [18]. More specific references will be given in the text. I summarise some principal definitions and results below. First, though, let me describe the main results.

Throughout this paper, R will be a ring with 1; the language will be that for (right R-) modules. All types will be complete types in a complete theory, T, of R-modules. The notation 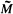is reserved for an extremely saturated model of T, inside which all “small” situations may be found. Thus, sets of parameters are just subsets of 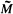, and all models will be elementary substructures of 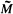. A positive primitive, or pp, formula 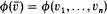is one which is equivalent to a formula of the form

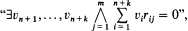
with the rij ∈ R.

Suppose that p and q are 1-types over a pure-injective model M.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 1 , March 1985 , pp. 202 - 219
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Baur, W., Elimination of quantifiers for modules, Israel Journal of Mathematics, vol. 25 (1976), pp. 64–70.Google Scholar
[2] Bumby, R. T., Modules which are isomorphic to submodules of each other, Archiv der Mathematik, vol. 16(1965), pp. 184–185.Google Scholar
[3] Fisher, E., Abelian structures. I, Abelian group theory (Proceedings, Las Cruces, New Mexico, 1976), Lecture Notes in Mathematics, vol. 616, Springer-Verlag, Berlin, 1977, pp. 270–322.Google Scholar
[4] Garavaglia, S., Direct product decomposition of theories of modules, this Journal, vol. 44 ( 1979), pp. 77–88.Google Scholar
[5] Garavaglia, S., Decomposition of totally transcendental modules, this Journal, vol.45 (1980), pp. 155–164.Google Scholar
[6] Garavaglia, S., Dimension and rank in the model theory of modules, preprint, Michigan State University, East Lansing, Michigan, 1980.Google Scholar
[7] Garavaglia, S., Forking in modules, Notre Dame Journal of Formal Logic, vol. 22 (1981), pp. 155–162.CrossRefGoogle Scholar
[8] Gruson, L. and Jensen, C. U., Dimensions cohomoloqiques reliées aux foncteurs , Séminaire d'Algèbre Paul Dubreilet Marie-Paule Malliavin, 33ème Année (1980), Lecture Notes in Mathematics, vol. 867, Springer-Verlag, Berlin, 1981, pp. 234–294.Google Scholar
[9] Kucera, T., preprint, 1980; also Ph.D. Thesis, McGill University, Montréal, 1984.Google Scholar
[10] Lascar, D., Ordre de Rudin-Keisler et poids dans les théories stables, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 28 (1982), pp. 413–430.Google Scholar
[11] Lascar, D. and Poizat, B., An introduction to forking, this Journal, vol. 44 (1979), pp. 330–350.Google Scholar
[12] Pillay, A., An introduction to stability theory, Oxford University Press, Oxford, 1983.Google Scholar
[13] Pillay, A. and Prest, M., Forking and pushouts in modules, Proceedings of the London Mathematical Society, ser. 3, vol. 46 (1983), pp. 365–384.Google Scholar
[14] Pillay, A. and Prest, M., Modules and stability theory, Preprint, Notre Dame University, Notre Dame, Indiana, and Yale University, New Haven, Connecticut, 1984.Google Scholar
[15] Poizat, B., Sous-groups définissables d'un groupe stable, this Journal, vol. 46(1981), pp. 137–146.Google Scholar
[16] Prest, M., Existentially complete prime rings, Journal of the London Mathematical Society, ser. 2, vol. 28(1983), pp. 238–246.CrossRefGoogle Scholar
[17] Prest, M., Pure-injectives and T-injective hulls of modules, preprint, 1981.Google Scholar
[18] Shelah, S., Classification theory, North-Holland, Amsterdam, 1978.Google Scholar
[19] Ziegler, M., Model theory of modules, Annals of Pure and Applied Logic, vol. 26 (1984), pp. 149–213.Google Scholar