Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-05-09T08:26:19.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Register machine proof of the theorem on exponential diophantine representation of enumerable sets

Published online by Cambridge University Press:  12 March 2014

J. P. Jones  and
Y. V. Matijasevič
J. P. Jones
Affiliation:
University of Calgary, Calgary, Alberta, Canada T2N 1N4
Y. V. Matijasevič
Affiliation:
Steklov Institute of Mathematics, Academy of Sciences of the USSR, Leningrad, USSR 191011
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of the present paper is to give a new, simple proof of the theorem of M. Davis, H. Putnam and J. Robinson [1961], which states that every recursively enumerable relation A(a1, …, an) is exponential diophantine, i.e. can be represented in the form

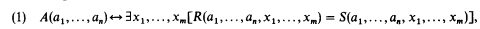
where a1 …, an, x1, …, xm range over natural numbers and R and S are functions built up from these variables and natural number constants by the operations of addition, A + B, multiplication, AB, and exponentiation, AB. We refer to the variables a1,…,an as parameters and the variables x1 …, xm as unknowns.

Historically, the Davis, Putnam and Robinson theorem was one of the important steps in the eventual solution of Hilbert's tenth problem by the second author [1970], who proved that the exponential relation, a = bc, is diophantine, and hence that the right side of (1) can be replaced by a polynomial equation. But this part will not be reproved here. Readers wishing to read about the proof of that are directed to the papers of Y. Matijasevič [1971a], M. Davis [1973], Y. Matijasevič and J. Robinson [1975] or C. Smoryński [1972]. We concern ourselves here for the most part only with exponential diophantine equations until §5 where we mention a few consequences for the class NP of sets computable in nondeterministic polynomial time.

Keywords

Primary 03D1003D2510N05
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 3 , September 1984 , pp. 818 - 829
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adleman, L. and Manders, K. [1975], Computational complexity of decision procedures for polynomials, 16th Annual Symposium on Foundations of Computer Science (Berkeley, California, 1975), IEEE Computer Society, Long Beach, California, 1975, pp. 169–177. MR 57 # 264.CrossRefGoogle Scholar
Adleman, L. and Manders, K. [1976], Diophantine complexity, 17th Annual Symposium on Foundations of Computer Science (Houston, Texas, 1976), IEEE Computer Society, Long Beach, California, 1976, pp. 81–88. MR 56 #7314.CrossRefGoogle Scholar
Barzdin′, Ja. M. [1963], On a certain class of Turing machines (Minsky machines), Algebra i Logika, vol. 1 (1962/63), no. 6, pp. 42–51. (Russian) MR 27 # 2415.Google Scholar
Börger, E. [1975], Recursively unsolvable algorithmic problems and related questions re-examined, ⊨ ISILC Logic Conference, Proceedings of the International Summer Institute and Logic Colloquium, Kiel, 1974 (Müller, G. H., Oberschelp, A. and Potthoff, K., editors), Lecture Notes in Mathematics, vol. 499, Springer-Verlag, Berlin, 1975, pp. 10–24. MR 58 # 10355.Google Scholar
Davis, M. [1953], Arithmetical problems and recursively enumerable predicates, this Journal, vol. 18 (1953), pp. 33–41. MR 14, 1052.Google Scholar
Davis, M. [1958], Computability and unsolvability, McGraw-Hill, New York, 1958. MR 23 # A1525.Google Scholar
Davis, M. [1973], Hubert's tenth problem is unsolvable, American Mathematical Monthly, vol. 80 (1973), pp. 233–269. MR 47 #6465.CrossRefGoogle Scholar
Davis, M. [1974], Computability, Lecture Notes, Courant Institute of Mathematical Sciences, New York University, New York, 1974. MR 50 #77.Google Scholar
Davis, M., Matijasevič, Y. V. and Robinson, J. [1976], Hubert's tenth problem. Diophantine equations: positive aspects of a negative solution, Mathematical developments arising from Hilbert problems, Proceedings of Symposia in Pure Mathematics, vol. 28, American Mathematical Society, Providence, Rhode Island, 1976, pp. 323–378. MR 55 #5522.CrossRefGoogle Scholar
Davis, M., Putnam, H. and Robinson, J. [1961], The decision problem for exponential diophantine equations, Annals of Mathematics, ser. 2, vol. 74 (1961), pp. 425–436. MR 24 # A3061.CrossRefGoogle Scholar
Fine, N. J. [1947], Binomial coefficients modulo a prime, American Mathematical Monthly, vol. 54 (1947), pp. 589–592. MR 9, 331.CrossRefGoogle Scholar
Hausner, M. [1983], Applications of a simple counting technique, American Mathematical Monthly, vol. 90 (1983), pp. 127–129.CrossRefGoogle Scholar
Hirose, K. and Iida, S. [1973], A proof of negative answer to Hubert's tenth problem, Proceedings of the Japan Academy, vol. 49 (1973), pp. 10–12. MR 58 #27750.Google Scholar
Jones, J. P. [1974], Recursive undecidability—an exposition, American Mathematical Monthly, vol. 81 (1974), pp. 724–738. MR 50 #9568.Google Scholar
Jones, J. P. [1978], Three universal representations of recursively enumerable sets, this Journal, vol. 43 (1978), pp. 335–351. MR 58 # 16226.Google Scholar
Jones, J. P. [1982]. Universal diophantine equation, this Journal, vol. 47 (1982), pp. 549–571.Google Scholar
Jones, J. P. and Matijasevič, Y. V. [1982], Exponential diophantine representation of recursively enumerable sets, Proceedings of the Herbrand Symposium, Logic Colloquium '81 (Stern, J., editor), Studies in Logic and the Foundations of Mathematics, vol. 107, North-Holland, Amsterdam, 1982, pp. 159–177.CrossRefGoogle Scholar
Karp, R. M. [1972], Reducibility among combinatorial problems, Complexity of computer computations (Miller, R. E. and Thatcher, J. W., editors), Plenum Press, New York, 1972, pp. 85–103. MR 51 #14644.CrossRefGoogle Scholar
Lambek, J. [1961], How to program an infinite abacus, Canadian Mathematical Bulletin, vol. 4 (1961), pp. 295–302. MR 24 #A2532.CrossRefGoogle Scholar
Lucas, E. [1878a], Sur les congruences des nombres eulériens et des coefficients différentiels des fonctions trigonométriques suivant un module premier, Bulletin de la Société Mathématique de France, vol. 6 (1877/78), pp. 49–54.CrossRefGoogle Scholar
Lucas, E. [1878b], Théorie des fonctions numériques simplement périodiques, American Journal of Mathematics, vol. 1 (1878), pp. 184–240; English translation available from the Fibonacci Association, San Jose University, San Jose, California, 1969.CrossRefGoogle Scholar
Matijasevič, Y. V. [1970], Enumerable sets are diophantine, Doklady Akademii Nauk SSSR, vol. 191 (1970), pp. 279–282; English translation with addendum, Soviet Mathematics: Doklady, vol. 11 (1970), pp. 354–357. MR 41 #3390.Google Scholar
Matijasevič, Y. V. [1971a], Diophantine representation of enumerable predicates, Izvestija Akademii Nauk SSSR Serija Matematičeskaja, vol. 35 (1971), pp. 3–30; English translation, Mathematics of the USSR—Izvestija, vol. 5 (1971), pp. 1–28. MR 43 #54.Google Scholar
Matijasevič, Y. V. [1971b], Diophantine representation of the set of prime numbers, Doklady Akademii Nauk SSSR, vol. 196 (1971), pp. 770–773; English translation, Soviet Mathematics: Doklady, vol. 12 (1971), pp. 249–254. MR 43 #1921.Google Scholar
Matijasevič, Y. V. [1971c], On recursive unsolvability of Hilbert's tenth problem, Proceedings of the Fourth International Congress for Logic, Methodology and Philosophy of Science (Bucharest, 1971), Studies in Logic and the Foundations of Mathematics, vol. 74, North-Holland, Amsterdam, 1973, pp. 89–110. MR 57 #5711.CrossRefGoogle Scholar
Matijasevič, Y. V. [1972], Diophantine sets, Uspehi Matematičeskih Nauk, vol. 27 (1972), no. 5 (167), pp. 185–222; English translation, Russian Mathematical Surveys, vol. 27 (1972), no. 5, pp. 124–164. MR 56 #109.Google Scholar
Matijasevič, Y. V. [1974], The existence of noneffectizable estimates in the theory of exponential diophantine equations, Zapiski Naučnyh Seminarov Leningradskogo Otdelenija Matematičeskogo Instituta im. V.A. Steklova (LOMI) Akademii Nauk SSSR, vol. 40(1974), pp. 77–93; English translation, Journal of Soviet Mathematics, vol. 8 (1977), pp. 299–311. MR 51 # 10225.Google Scholar
Matijasevič, Y. V. [1976], A new proof of the theorem on exponential diophantine representation of enumerable sets, Zapiski Naučnyh Seminarov Leningradskogo Otdelenija Matematičeskogo Instituta im. V.A. Steklova (LOMI) Akademii Nauk SSSR, vol. 60 (1976), pp. 75–89; English translation, Journal of Soviet Mathematics, vol. 14 (1980), pp. 1475–1486. MR 58 #27402.Google Scholar
Matijasevič, Y. V. [1977], A class of primality criteria formulated in terms of the divisibility of binomial coefficients, Zapiski Naučnyh Seminarov Leningradskogo Otdelenija Matematičeskogo Instituta im. V.A. Steklova (LOMI) Akademii Nauk SSSR, vol. 67 (1977), pp. 167–183; English translation, Journal of Soviet Mathematics, vol. 16 (1981), pp. 874–885. MR 57 #3060.Google Scholar
Matijasevič, Y. V. [1979], Algorithmic unsolvability of exponential diophantine equations in three unknowns, Studies in the Theory of Algorithms and Mathematical Logic (Markov, A. A. and Homic, V. I., editors), “Nauka”, Moscow, 1979, pp. 69–78; English translation, to appear in Selecta Mathematica Sovietica, vol. 3 (1983), no. 3. MR 81f: 03055.Google Scholar
Matijasevič, Y. and Robinson, J. [1975], Reduction of an arbitrary diophantine equation to one in 13 unknowns, Acta Arithmetica, vol. 27 (1975), pp. 521–553. MR 52 #8033.CrossRefGoogle Scholar
Melzak, Z. A. [1961], An informal arithmetical approach to computability and computation, Canadian Mathematical Bulletin, vol. 4 (1961), pp. 279–294. MR 27 #1364.CrossRefGoogle Scholar
Minsky, M. [1961], Recursive unsolvability of Post's problem of “tag” and other topics in the theory of Turing machines, Annals of Mathematics, ser. 2, vol. 74 (1961), pp. 437–455. MR 25 # 3825.CrossRefGoogle Scholar
Minsky, M. [1967], Computation: Finite and infinite machines, Prentice-Hall, Englewood Cliffs, New Jersey, 1967. MR 50 # 9050.Google Scholar
Robinson, J. [1952], Existential definability in arithmetic, Transactions of the American Mathematical Society, vol. 72 (1952), pp. 437–449. MR 14, 4.CrossRefGoogle Scholar
Robinson, J.,[1969], Diophantine decision problems, Studies in number theory (LeVeque, W. J., editor), MAA Studies in Mathematics, vol. 6, Mathematical Association of America, Buffalo, New York (distributed by Prentice-Hall, Englewood Cloiffs, New Jersey), pp. 76–116. MR 39 # 5364.Google Scholar
Shepherdson, J. C. and Sturgis, H. E. [1963], Computability of recursive functions, Journal of the Association for Computing Machinery, vol. 10 (1963), pp. 217–255. MR 27 # 1359.CrossRefGoogle Scholar
Smoryński, C. [1972], Notes on Hilbert's tenth problem: an introduction to unsolvability. Vol. 1, Department of Mathematics, University of Illinois at Chicago Circle, Chicago, Illinois, 1972.Google Scholar