Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-19T10:22:23.697Z Has data issue: false hasContentIssue false
  • English
  • Français

Ordinal definability in Jensen's model

Published online by Cambridge University Press:  12 March 2014

Włodzimierz Zadrożny
Włodzimierz Zadrożny*
Affiliation:
Mathematisches Institut der Universität Heidelberg, 6900 Heidelberg 1, West Germany
*
c/o Professor J. Books, 1320 Dartmouth, Denton, Texas 76201
Get access Rights & Permissions [Opens in a new window]

Extract

In [J] R. Jensen proved that any model of ZFC can be generically extended to a model of ZFC + (∃a ⊆ ω)(V = L[a]). This extension was made via a class P of forcing conditions. One can ask what can be said about the class HOD in such extensions. In particular one can ask whether V = HOD holds in Jensen's model. A full answer to this question is given by the following assertion:

Theorem. Let N = L[a] be given by forcing with Jensen's conditions (the classP).

Then:

1. N ⊨ V ≠ HOD,

2. N ⊨ (∀n < ω)(HODn + 1 ⊈ HODω).

3. N ⊨ (∀α ≥ ω)(HODα = HODω), or equivalently HODω + 1 = HODω.

The result is established by investigating homogeneity properties of certain complete Boolean algebras that are associated with the partial orderings of forcing conditions for coding using almost disjoint sets.

We explain shortly the first of our two technical results: It is rather well known that if we have a subset 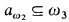then by performing threefold almost disjoint coding we come to a set a0 ⊆ ω such that 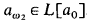; cf. [JS]. This is achieved by iterating over 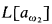almost disjoint forcing 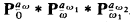. That means we first code 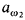by a subset 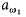, of [ω1ω2) using the almost disjoint forcing conditions 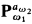. Then we code 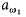by aω, contained in [ω, ω1), using forcing with 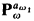over .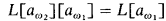

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 2 , June 1984 , pp. 608 - 620
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BS]Štěpanek, P. and Balcar, B., Embedding theorems for Boolean algebras and consistency results on ordinal definable sets, this Journal, vol. 42 (1977), pp. 64–76.Google Scholar
[G]Grigorieff, S., Intermediate submodels and generic extensions in set theory, Annals of Mathematics, ser. 2, vol. 101 (1975), pp. 447–490.CrossRefGoogle Scholar
[J]Beller, A., Jensen, R. and Welch, P., Coding the universe, Cambridge University Press, Cambridge, 1982.CrossRefGoogle Scholar
[J]Jech, T., Set theory, Academic Press, New York, 1978.Google Scholar
[JS]Jensen, R. and Solovay, R., Some applications of almost disjoint sets, Mathematical logic and foundations of set theory (Proceedings of an international colloquium, Jerusalem, 1968) (Bar-Hillel, Y., editor), North-Holland, Amsterdam, 1970, pp. 84–104.Google Scholar
[McAl]McAloon, K., Consistency results about ordinal definability, Annals of Mathematical Logic, vol. 2(1970/1971), pp. 449–467.CrossRefGoogle Scholar
[McA2]McAloon, K., On the sequence of models HODn, Fundamenta Mathematicae, vol. 82 (1974/1975), pp. 85–93.CrossRefGoogle Scholar
[MS]Myhill, J. and Scott, D., Ordinal definability, Axiomatic set theory, Proceedings of Symposia in Pure Mathematics, vol. 13, part 1, American Mathematical Society, Providence, Rhode Island, 1971, pp. 271–278.CrossRefGoogle Scholar
[Sa]Sakarovitch, J., Ph. D. Thesis, Université Paris-VII, Paris, 1977.Google Scholar
[St]Štěpanek, P., Cardinals in the inner model HOD, Higher set theory (Proceedings of a conference, Ober wolf ach, 1977), Lecture Notes in Mathematics, vol. 669, Springer-Verlag, Berlin, 1978, pp. 437–454.Google Scholar
[Z1]Zadrożny, W., Transfinite descending sequences of models HODα, Annals of Mathematical Logic, vol. 20 (1981), pp. 201–229.CrossRefGoogle Scholar
[Z2]Zadrożny, W., Iterating ordinal definability, Annals of Pure and Applied Logic, vol. 24 (1983), pp. 263–310.CrossRefGoogle Scholar