Let L be a first order predicate calculus with equality which has a fixed binary predicate symbol <. In this paper, we shall deal with quantifiers Cx, ∀x ≦ y, ∃x ≦ y defined as follows: CxA(x) is ∀y∃x(y ≦ x ∧ A(x)), ∀x ≦ yA{x) is ∀x(x ≦ y ⊃ A(x)), and ∃x ≦ yA(x) is ∃x(x ≦ y ∧ 4(x)). The expressions x̄, ȳ, … will be used to denote sequences of variables. In particular, x̄ stands for 〈x1, …, xn〉 and ȳ stands for 〈y1,…, ym〉 for some n, m. Also ∃x̄, ∀x̄ ≦ ȳ, … will be used to denote ∃x1 ∃x2 … ∃xn, ∀x1 ≦ y1 ∀x2 ≦ y2 … ∀xn ≦ yn, …, respectively. Let X be a set of formulas in L such that X contains every atomic formula and is closed under substitution of free variables and applications of propositional connectives ¬(not), ∧(and), ∨(or). Then, ∑(X) is the set of formulas of the form ∃x̄B(x̄), where B ∈ X, and Φ(X) is the set of formulas of the form

.

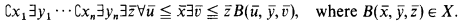Since X is closed under ∧, ∨, the two sets Σ(X) and Φ(X) are closed under ∧, ∨ in the following sense: for any formulas A and B in Σ(X) [Φ(X)], there are formulas in Σ(X)[ Φ(X)] which are obtained from A ∧ B and A ∨ B by bringing some quantifiers forward in the usual manner.