Introduction. This paper contains a new proof of the Church-Rosser theorem for the typed λ-calculus, which also applies to systems with infinitely long terms.

The ordinary proof of the Church-Rosser theorem for the general untyped calculus goes as follows (see [1]). If 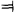is the binary reduction relation between the terms we define the one-step reduction 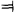1 in such a way that the following lemma is valid.

Lemma. For all terms a and b we have: a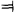b if and only if there is a sequence a = a0, …, an = b, n ≥ 0, such that ai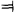iai + 1for 0 ≤ i < n.

We then prove the Church-Rosser property for the relation 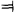1 by induction on the length of the reductions. And by combining this result with the above lemma we obtain the Church-Rosser theorem for the relation .

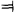Unfortunately when we come to infinite terms the above lemma is not valid anymore. The difficulty is that, assuming the hypothesis for the infinitely many premises of the infinite rule, there may not exist an upper bound for the lengths n of the sequences ai = a0, …, an = bi (i < α); cf. the infinite rule (iv) in §6.

A completely new idea in the case of the typed λ-calculus would be to exploit the type structure in the way Tait did in order to prove the normalization theorem. In this we succeed by defining a suitable predicate, the monovaluedness predicate, defined over the type structure and having some nice properties. The key notion permitting to define this predicate is the notion of I-form term (see below). This Tait-type proof has a merit, namely that it can be extended immediately to the case of infinite terms.