Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-26T06:30:26.724Z Has data issue: false hasContentIssue false
  • English
  • Français

The McKinsey axiom is not canonical

Published online by Cambridge University Press:  12 March 2014

Robert Goldblatt
Robert Goldblatt*
Affiliation:
Department of Mathematics, University of North Texas, Denton, Texas 76203
Get access Rights & Permissions [Opens in a new window]

Extract

The logic KM is the smallest normal modal logic that includes the McKinsey axiom

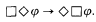
It is shown here that this axiom is not valid in the canonical frame for KM, answering a question first posed in the Lemmon-Scott manuscript [Lemmon, 1966].

The result is not just an esoteric counterexample: apart from interest generated by the long delay in a solution being found, the problem has been of historical importance in the development of our understanding of intensional model theory, and is of some conceptual significance, as will now be explained.

The relational semantics for normal modal logics first appeared in [Kripke, 1963], where a number of well-known systems were shown to be characterised by simple first-order conditions on binary relations (frames). This phenomenon was systematically investigated in [Lemmon, 1966], which introduced the technique of associating with each logic L a canonical frame 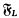which invalidates every nontheorem of L. If, in addition, each L-theorem is valid in 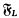, then L is said to be canonical. The problem of showing that L is determined by some validating condition C, meaning that the L-theorems are precisely those formulae valid in all frames satisfying C, can be solved by showing that 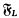satisfies C—in which case canonicity is also established. Numerous cases were studied, leading to the definition of a first-order condition Cφ associated with each formula φ of the form

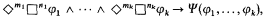
where Ψ is a positive modal formula.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 2 , June 1991 , pp. 554 - 562
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

van Benthem, J. F. A. K. [1975] A note on modal formulas and relational properties, this Journal, vol. 40, pp. 55–58.Google Scholar
van Benthem, J. F. A. K. [1980] Some kinds of modal completeness, Studia Logica, vol. 39, pp. 125–141.CrossRefGoogle Scholar
Fine, K. [1974] An incomplete logic containing S4, Theoria, vol. 40, pp. 23–29.CrossRefGoogle Scholar
Fine, K. [1975] Some connections between modal and elementary logic, Proceedings of the third Scandinavian logic symposium (Kanger, Stig, editor), Studies in Logic and Foundations of Mathematics, vol. 82, North-Holland, Amsterdam, pp. 15–31.CrossRefGoogle Scholar
Fine, K. [1975a] Normal forms in modal logic, Notre Dame Journal of Formal Logic, vol. 16, pp. 229–237.CrossRefGoogle Scholar
Goldblatt, R. I. [1975] Solution to a completeness problem of Lemmon and Scott, Notre Dame Journal of Formal Logic, vol. 16, pp. 405–408.CrossRefGoogle Scholar
Goldblatt, R. I. [1975a] First-order definability in modal logic, this Journal, vol. 40, pp. 35–40.Google Scholar
Goldblatt, R. I. [1976] Metamathematics of modal logic. I, II, Reports on Mathematical Logic, vol. 6, pp. 41–78, and vol. 7, pp. 21-52.Google Scholar
Goldblatt, R. I. [1990] On closure under canonical embedding algebras, Algebraic logic (Andréka, H.et al., editors), North-Holland, Amsterdam (to appear).Google Scholar
Kripke, S. [1963] Semantic analysis of modal logic. I: Normal propositional calculi, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 9, pp. 67–96.CrossRefGoogle Scholar
Lemmon, E. J. [1966] Intensional logic (by Lemmon, E. J. and Scott, Dana; preliminary draft of initial chapters by E. J. Lemmon, Stanford, 07 1966); finally published as An introduction to modal logic, American Philosophical Quarterly Monograph Series, vol. 11, Basil Blackwell, Oxford, 1977.Google Scholar
Sahlqvist, H. [1975] Completeness and correspondence in first and second order semantics for modal logic, Proceedings of the third Scandinavian logic symposium (Kanger, Stig, editor), Studies in Logic and Foundations of Mathematics, vol. 82, North-Holland, Amsterdam, pp. 110–143.CrossRefGoogle Scholar
Sambin, G., and Vaccaro, V. [1989] A new proof of Sahlqvist's theorem on modal definability and completeness, this Journal, vol. 54, pp. 992–999.Google Scholar
Thomason, S. K. [1972] Semantic analysis of tense logics, this Journal, vol. 37, pp. 150–158.Google Scholar
Thomason, S. K. [1974] An incompleteness theorem in modal logic, Theoria, vol. 40, pp. 30–34.CrossRefGoogle Scholar