Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-24T09:30:08.427Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the multiplicative semigroup of models of Peano arithmetic

Published online by Cambridge University Press:  12 March 2014

Roman Kossak ,
Mark Nadel  and
James Schmerl
Roman Kossak
Affiliation:
Baruch College, City University of New York, New York, New York 10010 Institute of Applied Mathematics and Statistics, Agricultural University of Warsaw, 02-766 Warsaw, Poland
Mark Nadel
Affiliation:
Mitre Corporation, Bedford, Massachusetts 01730
James Schmerl
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, Connecticut 06268
Get access Rights & Permissions [Opens in a new window]

Extract

In a model 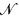of Peano arithmetic, the isomorphism type of the multiplicative semigroup uniquely determines the isomorphism type of the additive semigroup. In fact, for any prime p of 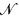, the function x ↦ px is an isomorphism of the additive semigroup with the multiplicative subsemigroup of powers of p. It was observed by Jensen and Ehrenfeucht [3] that for countable models of PA, the isomorphism type of the additive semigroup (or even the additive group) determines the isomorphism type of the multiplicative semigroup. (See Theorem 3 below.)

In this note we will show that the countability restriction cannot be dropped. First, we show (as Theorem 2) that for uncountable models of PA the isomorphism type of the additive group never determines the isomorphism type of the multiplicative semigroup. Our main result is Theorem 5 in which we show that the isomorphism type of the additive semigroup need not determine the isomorphism type of the multiplicative semigroup, thereby improving upon Harnik [2], where Theorem 5 is proved under the assumption of ♢. For completeness, a sketch of the proof of the Jensen-Ehrenfeucht result is included.

The history of this paper begins with Nadel's question, asked in 1981, whether the countability assumption can be eliminated in the Jensen-Ehrenfeucht theorem. Soon afterwards, Nadel obtained the strong counterexample of Theorem 2, which applied to the additive group rather than the additive semigroup. A result of Pabion [8] shows that such a strong result is not possible for the additive semigroup.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 3 , September 1989 , pp. 936 - 940
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cegielski, P., Théorie élémentaire de la multiplication des entiers naturels, Model theory and arithmetic (proceedings, Paris, 1979/1980), Lecture Notes in Mathematics, vol. 890, Springer-Verlag, Berlin, 1981, pp. 44–89.CrossRefGoogle Scholar
[2]Harnik, V., ω 1-like recursively saturated models of Presburger arithmetic, this Journal, vol. 51 (1986), pp. 421–429.Google Scholar
[3]Jensen, D. and Ehrenfeucht, A., Some problems in elementary arithmetic, Fundamenta Mathematicae, vol. 92 (1976), pp. 223–245.CrossRefGoogle Scholar
[4]Kaufmann, M., A rather classless model, Proceedings of the American Mathematical Society, vol. 62 (1977), pp. 330–333.CrossRefGoogle Scholar
[5]Lipshitz, L. and Nadel, M., The additive structure of models of arithmetic, Proceedings of the American Mathematical Society, vol. 68 (1978), pp. 331–336.CrossRefGoogle Scholar
[6]MacDowell, R. and Specker, E., Modelle der Arithmetik, Infinitistic methods (symposium, Warsaw, 1959), PWN, Warsaw, and Pergamon Press, Oxford, pp. 257–263.Google Scholar
[7]Nadel, M., The completeness of Peano multiplication, Israel journal of Mathematics, vol. 39(1981), pp. 225–233.CrossRefGoogle Scholar
[8]Pabion, J., Saturated models of Peano arithmetic, this Journal, vol. 47 (1982), pp. 625–637.Google Scholar
[9]Phillips, R. G., Omitting types in arithmetic and conservative extensions, Victoria symposium on nonstandard analysis, Lecture Notes in Mathematics, vol. 369, Springer-Verlag, Berlin, 1974, pp. 195–202.CrossRefGoogle Scholar
[10]Presburger, M., Über die Vollständigkeit eines gewissen Systems der Arithmetik ganzer Zahlen, in welche die Addition als einzige Operation hervortritt, Comptes-rendus du I congrès des mathématiciens des pays slaves (Warsaw, 1929), Ksia̧żnica Atlas T. N. S. W., Warsaw, 1930, pp. 92–101.Google Scholar
[11]Schmerl, J. H., Recursively saturated, rather classless models of Peano arithmetic, Logic Year 1979–80, Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin, 1981, pp. 268–282.CrossRefGoogle Scholar