Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-26T12:12:19.912Z Has data issue: false hasContentIssue false
  • English
  • Français

An existence theorem for a special ultrafilter when 𝔡 = 𝔠

Published online by Cambridge University Press:  12 March 2014

James J. Moloney
James J. Moloney*
Affiliation:
Marshall University, Huntington, West Virginia 25701
Get access Rights & Permissions [Opens in a new window]

Extract

For an ultrafilter 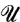, consider the ultrapower NN/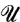. 〈an〉/ 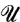is in the top sky of NN/ 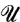if there exists a sequence 〈bn〉 ∈ NN such that

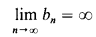
and

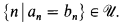
In [M2] we showed, assuming the Continuum Hypothesis, that there are exactly 10 c/p's (where c is the ring of real convergent sequences and p is a prime ideal of c). To get the lower bound we showed that there will be at least 10 c/p's in any model of ZFC where there exist both of the following kinds of ultrafilter:

(i) nonprincipal P-points,

(ii) non-P-points 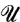such that when the top sky is removed from NN/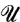, the remaining model has countable cofinality.

In [M2] we showed that the Continuum Hypothesis implies the existence of the ultrafilter in (ii). In this paper we show that its existence is implied by an axiom weaker than the Continuum Hypothesis, in fact weaker than Martin's Axiom, namely,

(*) If 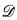is a subset of NN such that for any f: N → N there exists g ∈ 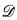such that g(n) > f(n) for all n, then ∣∣ = .

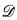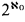Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 4 , December 1993 , pp. 1359 - 1364
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B]Booth, D., Ph.D. Thesis, University of Wisconsin, Madison, Wisconsin, 1969.Google Scholar
[C1]Cherlin, G., Rings of continuous functions: decision problems, Model theory of algebra and arithmetic 44–91, Lecture Notes in Mathematics, vol. 834, Springer-Verlag, Berlin, 1980.Google Scholar
[CD1]Cherlin, G. and Dickmann, M., Anneaux reél clos et anneaux des fonctions continues, Comptes Rendus de l'Académie des Sciences Série A–B, vol. 290 (1980), no. 1, pp. A1–A4.Google Scholar
[CD2]Cherlin, G. and Dickmann, M., Real closed rings II, model theory, Annals of Pure and Applied Logic, vol. 25 (1983), pp. 213–231.CrossRefGoogle Scholar
[CD3]Cherlin, G. and Dickmann, M., Real closed rings I, residue rings of rings of continuous functions, Fundamenta Mathematicae, vol. 126, (1986), pp. 147–183.CrossRefGoogle Scholar
[GJ]Gillman, L. and Jerison, M., Rings of continuous functions, D. Van Nostrand, Princeton, New Jersey, 1960.CrossRefGoogle Scholar
[GK]Gelfand, I. and Kolmogorov, A., On rings of continuous functions on topological spaces, Doklady Akademii Nauk SSSR, vol. 22 (1939), pp. 11–15.Google Scholar
[HJ]Hendriksen, M. and Johnson, D. G., On the structure of a class of Archimedean lattice-ordered algebras, Fundamenta Mathematicae, vol. 50 (1961), pp. 73–94.CrossRefGoogle Scholar
[HIJ]Hendriksen, M., Isbell, J., and Johnson, D. G., Residue class fields of lattice-ordered algebras, Fundamenta Mathematicae, vol. 50 (1961), pp. 107–117.CrossRefGoogle Scholar
[K1]Ketonen, J., On the existence of P-points in the Stone-Čech compactification of the integers, Fundamenta Mathematicae, vol. 97 (1976), pp. 91–94.CrossRefGoogle Scholar
[K2]Kochen, S., The model theory of local fields, Logic conference Kiel 1974, Lecture Notes in Mathematics, vol. 499, Springer-Verlag, Berlin, 1975, pp. 384–421.Google Scholar
[K3]Kohls, C. W., Prime ideals in rings of continuous functions, Illinois Journal of Mathematics, vol. 2 (1958), pp. 505–536.CrossRefGoogle Scholar
[K4]Kohls, C. W., Prime ideals in rings of continuous functions II, Duke Mathematical Journal, vol. 25 (1958), pp. 447–458.CrossRefGoogle Scholar
[M1]Moloney, J., First order theories of residue domains of rings of continuous functions, Thesis, Rutgers University, New Brunswick, New Jersey, 1986.Google Scholar
[M2]Kohls, C. W., Residue class domains of the ring of convergent sequences and of C∞([0,1], R), Pacific Journal of Mathematics, vol. 143 (1990), pp. 79–153.Google Scholar
[R]Rudin, W., Homogeneity problems in the theory of Čech compactifications, Duke Mathematical Journal, vol. 23 (1956), pp. 409–416.Google Scholar
[V]van Mill, J., An introduction to βω, Handbook of set theoretic topology, North-Holland, Amsterdam, 1984, pp. 503–567.CrossRefGoogle Scholar
[W]Wimmers, E., The Shelah P-point independence theorem, Israel Journal of Mathematics, vol. 43 (1982), pp. 28–48.CrossRefGoogle Scholar