Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-25T14:00:18.564Z Has data issue: false hasContentIssue false
  • English
  • Français

Degree theoretic definitions of the low2 recursively enumerable sets

Published online by Cambridge University Press:  12 March 2014

Rod Downey  and
Richard A. Shore
Rod Downey
Affiliation:
Mathematics Department, Victoria University of Wellington, Wellington, New Zealand, E-mail: Rod.Downey@vuw.ac.nz
Richard A. Shore
Affiliation:
Mathematics Department, Cornell University, Ithaca, New York 14853, E-mail: shore@math.cornell.edu
Get access Rights & Permissions [Opens in a new window]

Extract

The primary relation studied in recursion theory is that of relative complexity: A set or function A (of natural numbers) is reducible to one B if, given access to information about B, we can compute A. The primary reducibility is that of Turing, A ≤TB, where arbitrary (Turing) machines, φe, can be used; access to information about (the oracle) B is unlimited and the lengths of computations are potentially unbounded. Many other interesting reducibilities result from restricitng one or more of these facets of the procedure. Thus, for example, the strongest notion considered is one-one reducibility on sets: A ≤1B iff there is a one-one recursive (= effective) function f such that x Є A ⇔ f(x) Є B. Many-one (≤m) reducibility simply allows f to be many-one. Other intermediate reducibilities include truth-table (≤tt) and weak truth-table (≤wtt). The latter imposes a recursive bound f(x) on the information about B that can be used to compute A(x). The former also bounds the length of computations by requiring that the computation of A(x) from B halt in at most f(x) many steps.

Each such reducibility r defines a notion of degree, degr(A) = {B : A ≤rB ∧ B ≤rA}, and a corresponding structure 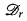of the r-degrees ordered by r-reducibility. (We typically denote the degree of A by a.) A major theme in recursion theory has been the investigation of the relation between a set's place in these orderings (the algebraic properties of its degree) and other algorithmic, set-theoretic or definability type notions of complexity. Important examples of such other notions include rates of growth of functions, the types of approximation procedures which converge to the given function or set and the (syntactic) complexity of defining the set (or function) in arithmetic or analysis.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 3 , September 1995 , pp. 727 - 756
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1973] Cooper, S. B., Minimal degrees and the jump operator, this Journal, vol. 38, pp. 249–271.Google Scholar
[1996] Cooper, S. B., Rigidity and definability in the noncomputable universe (to appear).Google Scholar
[1973] Degtev, A. N., tt- and m-degrees, Algebra and Logic, vol. 12, pp. 78–89.CrossRefGoogle Scholar
[1978] Degtev, A. N., Three theorems on tt-degrees, Algebra and Logic, vol. 17, pp. 187–194.CrossRefGoogle Scholar
[1993] Degtev, A. N., Array nonrecursive sets and lattice embeddings of the diamond, Illinois Journal of Mathematics, vol. 37, pp. 349–374.Google Scholar
[1989] Downey, R. G., Recursively enumerable m- and tt-degrees. I: The quantity of m-degrees, this Journal, vol. 54, pp. no. 2, 553–567.Google Scholar
[1990] Downey, R. G., Lattice nonembeddings and initial segments of the recursively enumerable degrees, Annals of Pure and Applied Logic, vol. 49, pp. 97–119.CrossRefGoogle Scholar
[1987] Downey, R. G. and Jockusch, C. Jr., T-degree, jump classes and strong reducibilities, Transactions of the American Mathematical Society, vol. 301, pp. 103–136.CrossRefGoogle Scholar
[1990] Downey, R. G., Jockusch, C., and Stob, M., Array nonrecursive sets and multiple permitting arguments, Recursion theory week (Ambos-Spies, K., et al., editors), Lecture Notes in Mathematics, vol. 1432, Springer-Verlag, Berlin, pp. 141–171.CrossRefGoogle Scholar
[1995] Downey, R. G. and Shore, R. A., Lattice embeddings below nonlow2 recursively enumerable degrees, Israel Journal of Mathematics (to appear).Google Scholar
[1989] Downey, R.G. and Slaman, T., Completely mitotic recursively enumerable degrees, Annals of Pure and Applied Logic, vol. 41, pp. 119–152.CrossRefGoogle Scholar
[1981] Epstein, R.L., Haas, R., and Kramer, R., Hierarchies of sets and degrees below 0′, Logic Year 1979-1980 (Lerman, M., et al., editors), Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin, pp. 32–48.CrossRefGoogle Scholar
[1989] Fejer, P. J. and Shore, R. A., A direct construction of a minimal tt-degree, Recursion theory week (Ambos-Spies, K., et al., editors), Lecture Notes in Mathematics, vo. 1432, Springer-Verlag, Berlin, pp. 187–204.CrossRefGoogle Scholar
[1972] Jockusch, C. G. Jr., Degrees in which the recursive sets are uniformly recursive, Canadian Journal of Mathematics, vol. 24, pp. 1092–1099.CrossRefGoogle Scholar
[1978] Jockusch, C.G. Jr., and Posner, D., Double jumps ofminimal degrees, this Journal, vol. 43, pp. 715–724.Google Scholar
[1972] Jockusch, C.G. Jr., and Soare, R. I., classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173, pp. 33–56.Google Scholar
[1979] Kobzev, G., On tt-degrees of recursively enumerable Turing degrees, Mathematics of the USSR-Sbornik, vol. 35, pp. 173–180.CrossRefGoogle Scholar
[1968] Lachlan, A., On the lattice of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 130, pp. 1–37.CrossRefGoogle Scholar
[1968a] Lachlan, A., Degrees of recursively enumerable sets which have no maximal supersets, this Journal, vol. 38, pp. 431–443.Google Scholar
[1975] Ladner, R. E., On the structure of polynomial-time reducibility, Journal of the Association for Computing Machinery, vol. 22, pp. 155–171.CrossRefGoogle Scholar
[1983] Lerman, M., Degrees of unsolvability, Springer-Verlag, Berlin.CrossRefGoogle Scholar
[1982] Maass, W., Recursively enumerable generic sets, this Journal, vol. 47, pp. 809–823.Google Scholar
[1966] Martin, D., Classes of recursively enumerable sets and degrees of unsolvability, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 12, pp. 295–310.CrossRefGoogle Scholar
[1970] Martin, D., and Pour.-El, M., Axiomatizable theories with few axiomatizable extensions, this Journal, vol. 35, pp. 205–209.Google Scholar
[1980a] Nerode, A., and Shore, R. A., Second order logic and first order theories of reducibility orderings, The Kleene symposium (Barwise, K. J.et al., editors), North-Holland, Amsterdam, pp. 181–200.CrossRefGoogle Scholar
[1980b] Nerode, A., and Shore, R. A., Reducibility orderings: Theories, definability and automorphisms, Annals of Mathematical Logic, vol. 18, pp. 61–89.CrossRefGoogle Scholar
[ta] Nies, A. and Shore, R. A., Interpreting true arithmetic in the theory of the tt and wtt degrees below 0′, in preparation.Google Scholar
[1981] Odifreddi, R, Strong reduciblities, Bulletin (New Series) of the American Mathematical Society, vol. 4, pp. 37–86.CrossRefGoogle Scholar
[1989] Odifreddi, R, Classical recursion theory, North-Holland, Amsterdam.Google Scholar
[ta] Odifreddi, R, Classical recursion theory, vol. 2, North-Holland, Amsterdam.Google Scholar
[1976] Shoenfield, J., Degrees of classes of r. e. sets, this Journal, vol. 41, pp. 695–696.Google Scholar
[1985] Shore, R. A., The structure of the degrees of unsolvability, Recursion theory (Nerode, A. and Shore, R. A., editors), Proceedings of Symposia in Pure Mathematics, vol. 42, American Mathematical Society, Providence, RI, pp. 33–51.CrossRefGoogle Scholar
[1990] Shore, R. A. and Slaman, T. A., Working below a lowi recursively enumerable degree, Archive for Mathematical Logic, vol. 29, pp. 201–211.CrossRefGoogle Scholar
[1993] Shore, R. A. and Slaman, T. A., Working below a high recursively enumerable degree, this Journal, vol. 58, pp. 824–859.Google Scholar
[1996] Slaman, T. and Woodin, H., Definability in degree structures, in preparation.Google Scholar
[1987] Soare, R. I., Recursively enumerable sets and degrees, Springer-Verlag, Berlin.CrossRefGoogle Scholar
[1969] Yates, C. E. M., On the degrees of index sets. II, Transactions of the American Mathematical Society, vol. 135, pp. 249–266.CrossRefGoogle Scholar