Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-26T11:30:03.171Z Has data issue: false hasContentIssue false
  • English
  • Français

Embeddability and the word problem

Published online by Cambridge University Press:  12 March 2014

Deko V. Dekov
Deko V. Dekov*
Affiliation:
Zahari Knjazeski 81, 6000 Stara Zagora, Bulgaria
Get access Rights & Permissions [Opens in a new window]

Extract

Let 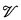be a finitely presented variety with operations Ω and let 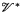be the variety having the same set of operations Ω but defined by the empty set of identities. A partial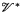-algebra 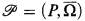is a set P with a set of mappings 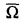containing for each n-ary operation f of Ω a mapping 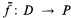, where D ⊆ Pn. An incomplete 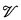-algebra is a partial 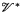-algebra 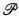which satisfies the defining identities of 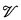, insofar as they can be applied to the partial operations of 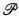(Trevor Evans [4, p. 67]). We call an incomplete 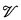-algebra a partial Evans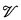-algebra if it can be embedded in a member of the variety .

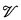If the class of all partial Evans 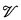-algebras is (first-order) finitely axiomatizable, then the word problem for the variety 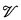is solvable. (Evans [4, 5]). In 1953 Evans [5, p. 79] raised the question of whether the converse is true. In this paper we show that the answer is in the negative.

Let CSg denote the variety of commutative semigroups. We call an incomplete CSg-algebra an incomplete commutative semigroup and we call a partial Evans CSg-algebra a partial Evans commutative semigroup. It is known (A. I. Malcev [9] see also Evans [6]) that the variety of commutative semigroups has solvable word problem. We show (Theorem 1) that the class of all partial Evans commutative semigroups is not finitely axiomatizable. Therefore the solvability of the word problem for the variety of commutative semigroups does not imply finite axiomatizability of the class of all partial Evans commutative semigroups.

Keywords

Primary 08A5508A5020M14
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 4 , December 1995 , pp. 1194 - 1198
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Andréka, H. and Németi, I., Generalization of the concept of variety and quasivariety to partial algebras through category theory, Dissertationes Mathematicae (Rozprawy Matematyczne) no. 204 (1983).Google Scholar
[2]Barwise, J. (editor), Handbook of mathematical logic, North-Holland, Amsterdam, 1977.Google Scholar
[3]Cohn, P. M., Universal algebra, Harper and Row, New York, 1965.Google Scholar
[4]Evans, T., The word problem for abstract algebras, Journal of the London Mathematical Society, vol. 26 (1951), pp. 64–71.CrossRefGoogle Scholar
[5]Evans, T., Embeddability and the word problem, Journal of the London Mathematical Society, vol. 28 (1953), pp. 76–80.CrossRefGoogle Scholar
[6]Evans, T., Some connections between residual finiteness, finite embeddability and the word problem, Journal of the London Mathematical Society, ser. 2, vol. 1 (1969), pp. 399–403.CrossRefGoogle Scholar
[7]Gensemer, S. H. and Weinert, H. I, On the embedding of partial groupoids into semigroups, Bayreuther Mathematische Schriften, vol. 28 (1989), pp. 139–163.Google Scholar
[8]Howie, J. M., An introduction to semigroup theory, Academic Press, London, 1976.Google Scholar
[9]Malcev, A. I., On homomorphisms onto finite groups, Ivanovskiǐ Gosudarstvennyǐ Pedagogicheskiǐ Institut Uchenye Zapiski, vol. 18 (1958), pp. 49–60; English translation, American Mathematical Society Translations ser. 2, vol. 119 (1983), pp. 67–79.Google Scholar
[10]Malcev, A. I., A few remarks on quasivarieties of algebraic systems, Algebra i Logika, vol. 5 (1966), no. 3, pp. 3–9; English translation, in Malcev, A. I., The metamathematics of algebraic systems, North-Holland, Amsterdam, 1971, pp. 416–421.Google Scholar
[11]Malcev, A. I., Algebraic systems, “Nauka”, Moscow, 1970 (Russian); English translation, Springer-Verlag, New York, 1973.Google Scholar