Abstract
This paper shows how the symmetric eigenproblem, which is the computationally most demanding part of numerous scientific and industrial applications, can be solved much more efficiently than by using algorithms currently implemented in Lapack routines.
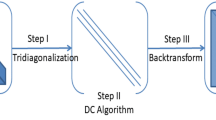
The main techniques used in the algorithm presented in this paper are (i) sophisticated blocking in the tridiagonalization, which leads to a two-sweep algorithm; and (ii) the computation of the eigenvectors of a band matrix instead of a tridiagonal matrix.
This new algorithm improves the locality of data references and leads to a significant improvement of the floating-point performance of symmetric eigensolvers on modern computer systems. Speedup factors of up to four (depending on the computer architecture and the matrix size) have been observed.
The work described in this paper was supported by the Special Research Program SFB F011 “AURORA” of the Austrian Science Fund.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Anderson., E., et al.: Lapack Users’ Guide, 2nd edn. SIAM Press, Philadelphia (1995)
Bischof, C.H., Lang, B., Sun, X.: Parallel Tridiagonalization through Two-Step Band Reduction. In: Proceedings of the Scalable High-Performance Computing Conference, pp. 23–27. IEEE Press, Washington (1994)
Bischof, C.H., Van Loan, C.F.: The WY Representation for Products of Householder Matrices. SIAM J. Sci. Comput 8, s2–s13 (1987)
Bischof, C.H., Lang, B., Sun, X.: A Framework for Symmetric Band Reduction, Technical Report ANL/MCS-P586-0496, Argonne National Laboratory (1996)
Bischof, C.H., Lang, B., Sun, X.: The SBR Toolbox–Software for Successive Band Reduction, Technical Report ANL/MCS-P587-0496, Argonne National Laboratory (1996)
Dongarra, J.J., Duff, I.S., Sorensen, D.C., van der Vorst, H.A.: Linear Algebra and Matrix Theory. SIAM Press, Philadelphia (1998)
Gansterer, W., Kvasnicka, D., Ueberhuber, C.: High Performance Computing in Material Sciences. Higher Level BLAS in Symmetric Eigensolvers, Technical Report AURORA TR1998-18, Vienna University of Technology (1998)
Gansterer, W., Kvasnicka, D., Ueberhuber, C.: High Performance Computing in Material Sciences. Numerical Experiments with Symmetric Eigensolvers, Technical Report AURORA TR1998-19, Vienna University of Technology (1998)
Schreiber, R., Parlett, B.: Block Reflectors: Theory and Computation. SIAM J. Numer. Anal. 25, 189–205 (1988)
Schreiber, R., Van Loan, C.: A Storage-Efficient WY Representation for Products of Householder Transformations. SIAM J. Sci. Stat. Comput. 10(1), 53–57 (1989)
Smith, B.T., et al.: Matrix Eigensystem Routines–Eispack Guide. Lecture Notesin Computer Science, vol. 6. Springer, Heidelberg (1976)
Ueberhuber, C.W.: Numerical Computation. Springer, Heidelberg (1997)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1999 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Gansterer, W.N., Kvasnicka, D.F., Ueberhuber, C.W. (1999). Multi-sweep Algorithms for the Symmetric Eigenproblem. In: Hernández, V., Palma, J.M.L.M., Dongarra, J.J. (eds) Vector and Parallel Processing – VECPAR’98. VECPAR 1998. Lecture Notes in Computer Science, vol 1573. Springer, Berlin, Heidelberg. https://doi.org/10.1007/10703040_3
Download citation
DOI: https://doi.org/10.1007/10703040_3
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-66228-0
Online ISBN: 978-3-540-48516-2
eBook Packages: Springer Book Archive