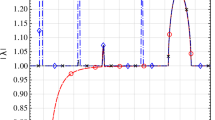
Abstract
The study of the motion of deformable models is one of the most important topics in computer animation. The model proposed by Terzopoulos et al. [16] uses Lagrange’s equation of motion and a variational principle to find the change of shape of deformable objects. We present in this work several methods for solving this equation numerically, and we study its complexity and stability, in order to find the best one. These methods have been classified in explicit and semi-implicit methods using central finite-difference methods and non-central finite-difference methods. We will see that the explicit methods are better than the semi-implicit ones because of lower computational cost in order to create the animation of non-highly deformable objects. Moreover, we will see that the behavior of non-central finite difference methods are better because they are stable. The study has been made for surfaces but can be easily generalizable to 3D curves and solids. To illustrate the applications we have displayed the animation of a held handkerchief and the free fall of a tablecloth over a table.
Partially supported by CICYT contract TIC-98-0302
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Agui, T., Nagao, Y., Nakajma, M.: An Expression Method of Cylindrical Cloth Objects-An Expression of Folds of a Sleeve using Computer Graphics. Trans. Soc. of Electronics, Information and Communications, J73-D-II 7, 1095–1097 (1990)
Aono, M.: A Wrinkle Propagation Model for Cloth. In: Proc. CG. Int’l, pp. 95–115. Springer, Heidelberg (1990)
Decaudin, P.: Geometric deformation by merging a 3d-object with a simple shape. In: Proc. of Graphics Interface, pp. 21–26 (1996)
do Carmo, M.P.: Differential Geometry of Curves and Surfaces. Prentice-Hall, USA (1976)
Dias, J.M.S., Galli, R., Palmer, P., Rebordao, J.M.: Deformable objects with real-time realistic behavior for virtual scenarios (in The Internet en 3D). Academic Press, London (1997)
Feynman, R.: Modeling the appearance of cloth. PhD thesis, Departament of Electrical Engineering and Computer Science. MIT, Cambridge (1986)
Greiner, G.: Surface Construction on Variational Principles. In: Laurent, P., Le Méhauté, A., Schumaker, L. (eds.) Wavelets, Images and Surface Fitting, pp. 277–286. A. K. Peters, Wellesley (1994)
Güdükbay, U., Özgüç, B.: Animation of deformable models. Computer-Aided Design 26(12), 868–875 (1994)
Hing, N.N., Grimsdale, R.L.: Computer Graphics Techniques for Modelling Cloth. IEEE Computer Graphics and Applications, 28–41 (1996)
Kimura, M., Saito, M., Shinya, M.: Surface deformation with differential geometric structures. Computer-Aided Geometric Design 13, 243–256 (1996)
Mascaró, M., Mir, A., Perales, F.: Visualization of dynamic deformations through triangular and square finite elements. In: CEIG 1999, pp. 47–61 (1999) An references therein (in Spanish)
Metaxas, D.N.: Physics-Based Deformable Models. Kluwer Academic Publishers, Dordrecht (1997)
Rudomin, I.J.: Simulating Cloth using a Mixed Geometry-Phisycal Method. Doctoral Dissertation, Dept. of Computer and Information Science, Univ. Of Pennsylvania (1990)
Serón, F.J., Badal, J., Sabadell, F.J.: A numerical laboratory for simulation and visualization of seismic wavefields. Geophysical Prospecting 44, 603–642 (1996)
Shabana, A.A.: Dinamics of Multibody Systems. John Wiley and Sons, Chichester (1988)
Terzopoulos, D., et al.: Elastically Deformable Models. Computer Graphics (Proc. Siggraph) 21(4), 205–214 (1987)
Terzopoulos, D., Witkin, A., Kass, M.: Deformable Models: Physically Based Models with Rigid and Deformable Components. IEEE Computer Graphics and Applications 13(7), 41–51 (1988)
Thalmann, N.M., Yang, Y.: Tecniques for Cloth Animation. In: M-Thalmann, N., Thalmann, D. (eds.) New Trends in Animation and Visualization, pp. 243–256. John Wiley & Sons, Chichester (1991)
Tsopelas, N.: Animation the Crumpling Behaviour of Garments. In: Proc. 2nd. Eurographics Workshop on Animation and Simulation, pp. 11–24. Blackwell, UK (1991)
Weil, J.: The Synthesis of Cloth Objects. In: Computer Graphics (Proc. Siggraph), vol. 20, pp. 49–54 (1986)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Copyright information
© 2000 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Palmer, P., Mir, A., González, M. (2000). Stability and Complexity Study of Animated Elastically Deformable Objects. In: Nagel, HH., Perales López, F.J. (eds) Articulated Motion and Deformable Objects. AMDO 2000. Lecture Notes in Computer Science, vol 1899. Springer, Berlin, Heidelberg. https://doi.org/10.1007/10722604_6
Download citation
DOI: https://doi.org/10.1007/10722604_6
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-67912-7
Online ISBN: 978-3-540-44591-3
eBook Packages: Springer Book Archive