Abstract
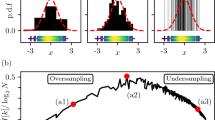
As resolving power increases, image features evolve in an iterative fashion; large scale features will persist, and finer and finer scale features are resolved at each increase in resolution. As such, the observation process is shown to overwhelm natural image statistics. Observation by a linear imaging process imposes natural image statistics to be of random multiplicative nature, rather than additive. The scaling behavior of the random process is driven by the gradient structure in the scene irradiance. From the general structure of multiplicative processes, image statistics are proven to follow a sequential fragmentation process. From these theoretical results, analytical forms for the distributions of image derivative filter responses and gradient magnitude are derived.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Geusebroek, J.M., Smeulders, A.W.M.: Fragmentation in the vision of scenes. In: Proc. 9th Int. Conf. Comput. Vision., vol. 1, pp. 130–135. IEEE Computer Society, Los Alamitos (2003)
Field, D.J.: Relations between the statistics of natural images and the response properties of cortical cells. J. Opt. Soc. Am. A 4, 2370–2393 (1987)
Mallat, S.G.: A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Machine Intell. 11, 674–693 (1989)
Ruderman, D.L., Bialek, W.: Statistics of natural images: Scaling in the woods. Phys. Rev. Let. 73, 814–817 (1994)
van der Schaaf, A., van Hateren, J.H.: Modelling the power spectra of natural images: Statistics and information. Vision Res. 36, 2759–2770 (1996)
Simoncelli, E.P.: Modeling the joint statistics of images in the wavelet domain. In: Proc. SPIE, vol. 3813, pp. 188–195. SPIE, Bellingham (1999)
Sigman, M., Cecchi, G.A., Gilbert, C.D., Magnasco, M.O.: On a common circle: Natural scenes and Gestalt rules. In: Proc. Natl. Acad. Sci. USA, vol. 98, pp. 1935–1940 (2001)
Schwartz, O., Simoncelli, E.P.: Natural signal statistics and sensory gain control. Nature Neurosci. 4, 819–825 (2001)
Grenander, U., Srivastava, A.: Probability models for clutter in natural images. IEEE Trans. Pattern Anal. Machine Intell. 23, 424–429 (2001)
Lee, A.B., Mumford, D., Huang, J.: Occlusion models for natural images: A statistical study of a scale-invariant dead leaves model. Int. J. Comput. Vision 41, 35–59 (2001)
Srivastava, A., Liu, X., Grenander, U.: Universal analytical forms for modeling image probabilities. IEEE Trans. Pattern Anal. Machine Intell. 24, 1200–1214 (2002)
Geusebroek, J.M., Smeulders, A.W.M.: A physical explanation for natural image statistics. In: Chantler, M. (ed.) Proceedings of the 2nd International Workshop on Texture Analysis and Synthesis (Texture 2002), Heriot-Watt University, pp. 47–52 (2002)
Srivastava, A., Lee, A.B., Simoncelli, E.P., Zhu, S.C.: On advances in statistical modeling of natural images. J. Math. Imaging Vision 18, 17–33 (2003)
Koenderink, J.J.: The structure of images. Biol. Cybern. 50, 363–370 (1984)
Havlin, S., Selinger, R.B., Schwartz, M., Stanley, H.E., Bunde, A.: Random multiplicative processes and transport in structures with correlated spatial disorder. Phys. Rev. Let. 61, 1438–1441 (1988)
Castaing, B., Dubrulle, B.: Fully developed turbulence: A unifying point of view. J. Phys. II (France) 5, 895–899 (1995)
Arneodo, A., Bacry, E., Manneville, S., Muzy, J.F.: Analysis of random cascades using space-scale correlation functions. Phys. Rev. Let. 80, 708–711 (1998)
Brown, W.K.: A theory of sequential fragmentation and its astronomical applications. J. Astrophys. Astr. 10, 89–112 (1989)
Papoulis, A., Pillai, S.U.: Probability, Random Variables, and Stochastic Processes, 4th edn. McGraw-Hill, New York (2002)
Benzi, R., Biferale, L., Crisanti, A., Paladin, G., Vergassola, M., Vulpiani, A.: A random process for the construction of multiaffine fields. Physica D 65, 352–358 (1993)
Havlin, S., Schwartz, M., Selinger, R.B., Bunde, A., Stanley, H.E.: Universality classes for diffusion in the presence of correlated spatial disorder. Phys. Rev. A 40, 1717–1719 (1989)
Redner, S.: Random multiplicative processes: An elementary tutorial. Am. J. Phys. 58, 267–273 (1990)
Levy, M., Solomon, S.: Power laws are logaritmic boltzmann laws. Int. J. Mod. Phys. C 7, 595–601 (1996)
Sornette, D., Cont, R.: Convergent multiplicative processes repelled from zero: Power-laws and truncated power-laws. J. Phys. I (France) 7, 431–444 (1997)
Feller, W.: An Introduction to Probability Theory and its Applications, vol. 2. John Wiley and Sons, New York (1971)
Gnedenko, B.V., Kolmogorov, A.N.: Limit Distributions for Sums of Independent Random Variables. Addison-Wesley, Reading (1968)
Dana, K.J., van Ginneken, B., Nayar, S.K., Koenderink, J.J.: Reflectance and texture of real world surfaces. ACM Trans Graphics 18, 1–34 (1999)
van Hateren, J.H., van der Schaaf, A.: Independent component filters of natural images compared with simple cells in primary visual cortex. Proc. R. Soc. Lond. B 265, 359–366 (1998)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Geusebroek, JM. (2005). The Stochastic Structure of Images. In: Kimmel, R., Sochen, N.A., Weickert, J. (eds) Scale Space and PDE Methods in Computer Vision. Scale-Space 2005. Lecture Notes in Computer Science, vol 3459. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11408031_28
Download citation
DOI: https://doi.org/10.1007/11408031_28
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-25547-5
Online ISBN: 978-3-540-32012-8
eBook Packages: Computer ScienceComputer Science (R0)