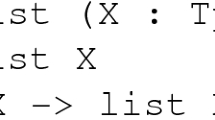Abstract
Fiore, Plotkin and Turi provided a definition of binding signature and characterised the presheaf of terms generated from a binding signature by an initiality property. Tanaka did for linear binders what Fiore et al did for cartesian binders. They used presheaf categories to model variable binders for contexts, with leading examples given by the untyped ordinary and linear λ-calculi. Here, we give an axiomatic framework that includes their works on cartesian and linear binders, and moreover their assorted variants, notably including the combined cartesian and linear binders of the Logic of Bunched Implications. We provide a definition of binding signature in general, extending the previous ones and yielding a definition for the first time for the example of Bunched Implications, and we characterise the presheaf of terms generated from the binding signature. The characterisation requires a subtle analysis of a strength of a binding signature over a substitution monoidal structure on the presheaf category.
This work has been done with the support of EPSRC grants GR/N64571/01 and GR/586372/01, A Theory of Effects for Programming Languages.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Fiore, M.: Semantic analysis of normalisation by evaluation for typed lambda calculus. In: Proc. PPDP 2002, pp. 26–37. ACM Press, New York (2002)
Fiore, M., Plotkin, G., Turi, D.: Abstract syntax and variable binding. In: Proc. LICS 1999, pp. 193–202. IEEE Press, Los Alamitos (1999)
Gabbay, M., Pitts, A.M.: A new approach to abstract syntax involving binders. In: Proc. LICS 1999, pp. 214–224. IEEE Press, Los Alamitos (1999)
Hofmann, M.: Semantical analysis of higher-order abstract syntax. In: Proc. LICS 1999, pp. 204–213. IEEE Press, Los Alamitos (1999)
Hyland, M., Power, A.J.: Pseudo-commutative monads and pseudo-closed 2-categories. J. Pure and Applied Algebra 175, 141–185 (2002)
Kelly, G.M.: Basic Concepts of Enriched Category Theory, London Math. Soc. Lecture Notes Series 64. Cambridge University Press, Cambridge (1982)
Mac Lane, S.: Categories for the Working Mathematician. Springer, Heidelberg (1971)
Miculan, M., Scagnetto, I.: A framework for typed HOAS and semantics. In: Proc. PPDP 2003, pp. 184–194. ACM Press, New York (2003)
Plotkin, G.D., Power, A.J.: Algebraic Operations and Generic Effects. In: Proc. MFCSIT 2000, Applied Categorical Structures, vol. 11, pp. 69–94 (2003)
Power, A.J.: Enriched Lawvere theories. Theory and Applications of Categories 6, 83–93 (1999)
Power, A.J.: A Unified Category-Theoretic Approach to Variable Binding. In: Proc. MERLIN 2003. ACM Digital Library, New York (2003)
Power, A.J.: Countable Lawvere theories and Computational Effects (Submitted)
Power, A.J., Tanaka, M.: Pseudo-Distributive Laws and Axiomatics for Variable Binding (Submitted)
Pym, D.: The Semantics and Proof Theory of the Logic of Bunched Implications. Applied Logic Series. Kluwer, Dordrecht (2002)
Tanaka, M.: Abstract syntax and variable binding for linear binders. In: Nielsen, M., Rovan, B. (eds.) MFCS 2000. LNCS, vol. 1893, pp. 670–679. Springer, Heidelberg (2000)
Tanaka, M.: Pseudo-Distributive Laws and a Unified Framework for Variable Binding. Edinburgh Ph.D. thesis (2004)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Power, J., Tanaka, M. (2005). Binding Signatures for Generic Contexts. In: Urzyczyn, P. (eds) Typed Lambda Calculi and Applications. TLCA 2005. Lecture Notes in Computer Science, vol 3461. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11417170_23
Download citation
DOI: https://doi.org/10.1007/11417170_23
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-25593-2
Online ISBN: 978-3-540-32014-2
eBook Packages: Computer ScienceComputer Science (R0)