Abstract
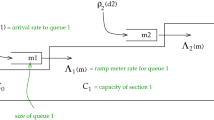
We present closed form analytical results to show the throughput performance of a discrete-window closed-loop conveyors system serving a user-specified set of stations with intermixed load/unload stations. The buffer capacity at the unloading stations is finite; loads that encounter a full buffer (i.e., blocked loads) are assumed to recirculate around the loop to try again. Given the job flow and routing data as well as the configuration of the conveyor loop, we present an analytical approach to approximate the expected overflow of loads on the conveyor (due to blocked loads). Given the expected overflow, we also show the stability condition for the conveyor system.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Bozer, Y.A., Hsieh, Y.J.: Throughput Performance Analysis and Machine Layout for Discrete-Space Closed-Loop Conveyors. IIE Transactions 37, 77–89 (2005)
Bozer, Y.A., Hsieh, Y.J.: Expected Waiting Times at Loading Stations in Discretespace Closed-Loop Conveyors. European Journal of Operation Research 155, 516–532 (2004)
Fredericks, A.A., Reisner, G.A.: Approximation to Stochastic Service Systems with an Application to a Retrial Model. The Bell System Technical Journal 58, 557–576 (1979)
Greenberg, B.S.: M/G/1 Queueing Systems with Returning Customers. Journal of Applied Probability 26(1), 152–163 (1989)
Greenberg, B.S., Wolff, R.W.: An Upper Bound on the Performance of Queues with Returning Customers. Journal of Applied Probability 24(2), 466–475 (1987)
Palm, C.: Intensitatsschwankungen im Fernsprecheverkehr. Ericsson Technics 44, 1–8 (1943)
Pourbabai, B., Sonderman, D.: A Stochastic Recirculation System with Random Access. European Journal of Operational Research 21, 367–378 (1985)
Pourbabai, B.: Markovian Queueing Systems with Retrials and Heterogeneous Servers. Computational Mathematics Application 13, 917–923 (1987)
Sonderman, D.: An Analytical Model for Recirculating Conveyors with Stochastic Inputs and Outputs. International Journal of Production Research 20, 591–605 (1982)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Hsieh, YJ., Bozer, Y.A. (2005). Analytical Modeling of Closed-Loop Conveyors with Load Recirculation. In: Gervasi, O., et al. Computational Science and Its Applications – ICCSA 2005. ICCSA 2005. Lecture Notes in Computer Science, vol 3483. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11424925_47
Download citation
DOI: https://doi.org/10.1007/11424925_47
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-25863-6
Online ISBN: 978-3-540-32309-9
eBook Packages: Computer ScienceComputer Science (R0)