Skip to main content
Springer Nature Link
Log in

The Multi-radius Cover Problem

  • Conference paper
Algorithms and Data Structures (WADS 2005)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 3608))

Included in the following conference series:

  • 1104 Accesses

Abstract

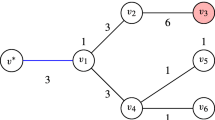
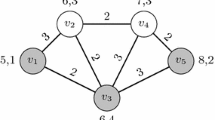
Let G = (V,E) be a graph with a non-negative edge length l u,v for every (u,v) ∈ E. The vertices of G represent locations at which transmission stations are positioned, and each edge of G represents a continuum of demand points to which we should transmit. A station located at v is associated with a set R v of allowed transmission radii, where the cost of transmitting to radius r ∈ R v is given by c v (r). The multi-radius cover problem asks to determine for each station a transmission radius, such that for each edge (u,v) ∈ E the sum of the radii in u and v is at least l u,v , and such that the total cost is minimized.

In this paper we present LP-rounding and primal-dual approximation algorithms for discrete and continuous variants of multi-radius cover. Our algorithms cope with the special structure of the problems we consider by utilizing greedy rounding techniques and a novel method for constructing primal and dual solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Bar-Yehuda, R., Even, S.: A linear-time approximation algorithm for the weighted vertex cover problem. Journal of Algorithms 2, 198–203 (1981)

    Article  MATH  MathSciNet  Google Scholar 

  2. Bar-Yehuda, R., Even, S.: A local-ratio theorem for approximating the weighted vertex cover problem. Annals of Discrete Mathematics 25, 27–46 (1985)

    MathSciNet  Google Scholar 

  3. Chuzhoy, J., Naor, J.: Covering problems with hard capacities. In: Proceedings of the 43rd Annual Symposium on Foundations of Computer Science, pp. 481–489 (2002)

    Google Scholar 

  4. Dinur, I., Safra, S.: The importance of being biased. In: Proceedings of the 34th Annual ACM Symposium on Theory of Computing, pp. 33–42 (2002)

    Google Scholar 

  5. Guha, S., Hassin, R., Khuller, S., Or, E.: Capacitated vertex covering. Journal of Algorithms 48, 257–270 (2003)

    Article  MATH  Google Scholar 

  6. Halperin, E.: Improved approximation algorithms for the vertex cover problem in graphs and hypergraphs. SIAM Journal on Computing 31, 1608–1623 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  7. Hassin, R., Levin, A.: The minimum generalized vertex cover problem. In: Proceedings of the 11th Annual European Symposium on Algorithms, pp. 289–300 (2003)

    Google Scholar 

  8. Hochbaum, D.S.: Approximation algorithms for the set covering and vertex cover problems. SIAM Journal on Computing 11, 555–556 (1982)

    Article  MATH  MathSciNet  Google Scholar 

  9. Williamson, D.P.: The primal-dual method for approximation algorithms. Mathematical Programming, Series B 91, 447–478 (2002)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Tel-Aviv University, Tel-Aviv, 69978, Israel

    Refael Hassin & Danny Segev

Authors
  1. Refael Hassin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Danny Segev
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Carleton University, Ottawa, Canada

    Frank Dehne

  2. Cheriton School of Computer Science, University of Waterloo, N2L 3G1, Waterloo, Ont., Canada

    Alejandro López-Ortiz

  3. School of Computer Science, Carleton University, 1125 Colonel By Drive, K1S 5B6, Ottawa, Canada

    Jörg-Rüdiger Sack

Rights and permissions

Reprints and permissions

Copyright information

© 2005 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Hassin, R., Segev, D. (2005). The Multi-radius Cover Problem. In: Dehne, F., López-Ortiz, A., Sack, JR. (eds) Algorithms and Data Structures. WADS 2005. Lecture Notes in Computer Science, vol 3608. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11534273_4

Download citation

  • DOI: https://doi.org/10.1007/11534273_4

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-28101-6

  • Online ISBN: 978-3-540-31711-1

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics