Skip to main content
Springer Nature Link
Log in

On Trip Planning Queries in Spatial Databases

  • Conference paper
Advances in Spatial and Temporal Databases (SSTD 2005)

Part of the book series: Lecture Notes in Computer Science ((LNISA,volume 3633))

Included in the following conference series:

  • 2586 Accesses

Abstract

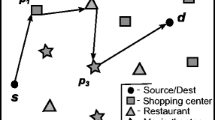
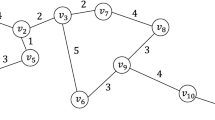
In this paper we discuss a new type of query in Spatial Databases, called the Trip Planning Query (TPQ). Given a set of points of interest P in space, where each point belongs to a specific category, a starting point S and a destination E, TPQ retrieves the best trip that starts at S, passes through at least one point from each category, and ends at E. For example, a driver traveling from Boston to Providence might want to stop to a gas station, a bank and a post office on his way, and the goal is to provide him with the best possible route (in terms of distance, traffic, road conditions, etc.). The difficulty of this query lies in the existence of multiple choices per category. In this paper, we study fast approximation algorithms for TPQ in a metric space. We provide a number of approximation algorithms with approximation ratios that depend on either the number of categories, the maximum number of points per category or both. Therefore, for different instances of the problem, we can choose the algorithm with the best approximation ratio, since they all run in polynomial time. Furthermore, we use some of the proposed algorithms to derive efficient heuristics for large datasets stored in external memory. Finally, we give an experimental evaluation of the proposed algorithms using both synthetic and real datasets.

This work was partially supported by NSF grants IIS-0133825, IIS-0308213, CCR-0311430, and ITR CCR-0325630.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Arora, S.: Polynomial time approximation schemes for euclidean tsp and other geometric problems. In: FOCS, p. 2 (1996)

    Google Scholar 

  2. Arora, S.: Approximation schemes for NP-hard geometric optimization problems: A survey. Mathematical Programming (2003)

    Google Scholar 

  3. Bansal, N., Blum, A., Chawla, S., Meyerson, A.: Approximation algorithms for deadline-tsp and vehicle routing with time-windows. In: STOC, pp. 166–174 (2004)

    Google Scholar 

  4. Beckmann, N., Kriegel, H., Schneider, R., Seeger, B.: The R*-tree: An efficient and robust access method for points and rectangles. In: SIGMOD, pp. 220–231 (1990)

    Google Scholar 

  5. Benetis, R., Jensen, C.S., Karciauskas, G., Saltenis, S.: Nearest neighbor and reverse nearest neighbor queries for moving objects. In: IDEAS, pp. 44–53 (2002)

    Google Scholar 

  6. Berchtold, S., Böhm, C., Keim, D.A., Kriegel, H.-P.: A cost model for nearest neighbor search in high-dimensional data space. In: PODS, pp. 78–86 (1997)

    Google Scholar 

  7. Böhm, C.: A cost model for query processing in high dimensional data spaces. TODS 25(2), 129–178 (2000)

    Article  Google Scholar 

  8. Brinkhoff, T.: A framework for generating network-based moving objects. GeoInformatica 6(2), 153–180 (2002)

    Article  MATH  Google Scholar 

  9. Christofides, N.: Worst-case analysis of a new heuristic for the travelling salesman problem. Technical report, Computer Science Department,Carnegie Mellon University (1976)

    Google Scholar 

  10. Cormen, T., Leiserson, C., Rivest, R., Stein, C.: Introduction to Algorithms. The MIT Press, Cambridge (1997)

    Google Scholar 

  11. Dumitrescu, A., Mitchell, J.S.B.: Approximation algorithms for tsp with neighborhoods in the plane. In: SODA, pp. 38–46 (2001)

    Google Scholar 

  12. Egenhofer, M.J.: What’s special about spatial?: database requirements for vehicle navigation in geographic space. In: SIGMOD, pp. 398–402 (1993)

    Google Scholar 

  13. Even, G., Kortsarz, G.: An approximation algorithm for the group steiner problem. In: SODA, pp. 49–58 (2002)

    Google Scholar 

  14. Fakcharoenphol, J., Rao, S., Talwar, K.: A tight bound on approximating arbitrary metrics by tree metrics. Journal of Computer and System Sciences 69(3), 485–497 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  15. Ferhatosmanoglu, H., Stanoi, I., Agrawal, D., Abbadi, A.E.: Constrained nearest neighbor queries. In: Jensen, C.S., Schneider, M., Seeger, B., Tsotras, V.J. (eds.) SSTD 2001. LNCS, vol. 2121, pp. 257–278. Springer, Heidelberg (2001)

    Chapter  Google Scholar 

  16. Garg, N., Konjevod, G., Ravi, R.: A polylogarithmic approximation algorithm for the group steiner tree problem. Journal of Algorithms 37(1), 66–84 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  17. Hartmut Guting, R., Bohlen, M.H., Erwig, M., Jensen, C.S., Lorentzos, N.A., Schneider, M., Vazirgiannis, M.: A foundation for representing and querying moving objects. TODS 25(1), 1–42 (2000)

    Article  Google Scholar 

  18. Guttman, A.: R-trees: A dynamic index structure for spatial searching. In: SIGMOD, pp. 47–57 (1984)

    Google Scholar 

  19. Hjaltason, G., Samet, H.: Distance Browsing in Spatial Databases. TODS 24(2), 265–318 (1999)

    Article  Google Scholar 

  20. Ihler, E.: Bounds on the Quality of Approximate Solutions to the Group Steiner Problem. Technical report, Institut fur Informatik,Uiversity Freiburg (1990)

    Google Scholar 

  21. Kolahdouzan, M.R., Shahabi, C.: Voronoi-based k nearest neighbor search for spatial network databases. In: VLDB, pp. 840–851 (2004)

    Google Scholar 

  22. Korn, F., Muthukrishnan, S.: Influence sets based on reverse nearest neighbor queries. In: SIGMOD, pp. 201–212 (2000)

    Google Scholar 

  23. Motwani, R., Raghavan, P.: Randomized Algorithms. Cambridge University Press, Cambridge (1995)

    MATH  Google Scholar 

  24. Myung, Y.S., Lee, C.H., Tcha, D.W.: On the Generalized Minimum Spanning Tree Problem. Networks 26, 231–241 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  25. Digital Chart of the World Server, http://www.maproom.psu.edu/dcw/

  26. Papadias, D., Shen, Q., Tao, Y., Mouratidis, K.: Group nearest neighbor queries. In: ICDE, pp. 301–312 (2004)

    Google Scholar 

  27. Papadias, D., Zhang, J., Mamoulis, N., Tao, Y.: Query processing in spatial network databases. In: VLDB, pp. 802–813 (2003)

    Google Scholar 

  28. Papadopoulos, A., Manolopoulos, Y.: Performance of nearest neighbor queries in r-trees. In: Afrati, F.N., Kolaitis, P.G. (eds.) ICDT 1997. LNCS, vol. 1186, pp. 394–408. Springer, Heidelberg (1996)

    Google Scholar 

  29. Roussopoulos, N., Kelley, S., Vincent, F.: Nearest neighbor queries. In: SIGMOD, pp. 71–79 (1995)

    Google Scholar 

  30. Shahabi, C., Kolahdouzan, M.R., Sharifzadeh, M.: A road network embedding technique for k-nearest neighbor search in moving object databases. In: GIS, pp. 94–100 (2002)

    Google Scholar 

  31. Sharifzadeh, M., Kolahdouzan, M., Shahabi, C.: The Optimal Sequenced Route Query. Technical report, Computer Science Department, University of Southern California (2005)

    Google Scholar 

  32. Shekhar, S., Liu, D.-R.: Ccam: A connectivity-clustered access method for networks and network computations. TKDE 9(1), 102–119 (1997)

    Google Scholar 

  33. TSP Home Web Site, http://www.tsp.gatech.edu/

  34. Spielman, D.A., Teng, S.-H.: Smoothed analysis of algorithms: why the simplex algorithm usually takes polynomial time. In: STOC, pp. 296–305 (2001)

    Google Scholar 

  35. U.S. Geological Survey, http://www.usgs.gov/

  36. Tao, Y., Papadias, D.: Time-parameterized queries in spatio-temporal databases. In: SIGMOD, pp. 334–345 (2002)

    Google Scholar 

  37. Tao, Y., Papadias, D., Shen, Q.: Continuous nearest neighbor search. In: VLDB, pp. 287–298 (2002)

    Google Scholar 

  38. Tao, Y., Zhang, J., Papadias, D., Mamoulis, N.: An Efficient Cost Model for Optimization of Nearest Neighbor Search in Low and Medium Dimensional Spaces. TKDE 16(10), 1169–1184 (2004)

    Google Scholar 

  39. Theodoridis, Y., Stefanakis, E., Sellis, T.: Efficient cost models for spatial queries using r-trees. TKDE 12(1), 19–32 (2000)

    Google Scholar 

  40. Vazirgiannis, M., Wolfson, O.: A spatiotemporal model and language for moving objects on road networks. In: Jensen, C.S., Schneider, M., Seeger, B., Tsotras, V.J. (eds.) SSTD 2001. LNCS, vol. 2121, pp. 20–35. Springer, Heidelberg (2001)

    Chapter  Google Scholar 

  41. Xiong, X., Mokbel, M.F., Aref, W.G.: Sea-cnn: Scalable processing of continuous k-nearest neighbor queries in spatio-temporal databases. In: ICDE, pp. 643–654 (2005)

    Google Scholar 

  42. Xiong, X., Mokbel, M.F., Aref, W.G., Hambrusch, S.E., Prabhakar, S.: Scalable spatio-temporal continuous query processing for location-aware services. In: SSDBM, pp. 317–327 (2004)

    Google Scholar 

  43. Yiu, M.L., Mamoulis, N.: Clustering objects on a spatial network. In: SIGMOD, pp. 443–454 (2004)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Computer Science Department, Boston University,  

    Feifei Li, Dihan Cheng, Marios Hadjieleftheriou, George Kollios & Shang-Hua Teng

Authors
  1. Feifei Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dihan Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Marios Hadjieleftheriou
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. George Kollios
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Shang-Hua Teng
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Institute of Computing, CP 6176, University of Campinas, 13084-971, Campinas, Brazil

    Claudia Bauzer Medeiros

  2. National Center for Geographic Information and Analysis and Department of Spatial Information Science and Engineering, University of Maine, Boardman Hall, ME 04469-5711, Orono, USA

    Max J. Egenhofer

  3. Purdue University,  

    Elisa Bertino

Rights and permissions

Reprints and permissions

Copyright information

© 2005 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Li, F., Cheng, D., Hadjieleftheriou, M., Kollios, G., Teng, SH. (2005). On Trip Planning Queries in Spatial Databases. In: Bauzer Medeiros, C., Egenhofer, M.J., Bertino, E. (eds) Advances in Spatial and Temporal Databases. SSTD 2005. Lecture Notes in Computer Science, vol 3633. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11535331_16

Download citation

  • DOI: https://doi.org/10.1007/11535331_16

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-540-28127-6

  • Online ISBN: 978-3-540-31904-7

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics