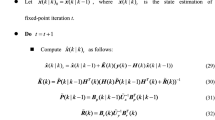Abstract
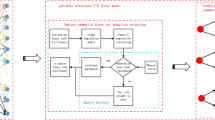
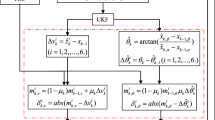
A novel adaptive algorithm for tracking maneuvering targets is proposed in this paper. The algorithm is implemented with fuzzy filtering and unscented transformation. A fuzzy system allows the filter to tune the magnitude of maximum accelerations to adapt to different target maneuvers. Unscented transformation act as a method for calculating the statistics of a random vector. A bearing-only tracking scenario simulation results show the proposed algorithm has a robust advantage over a wide range of maneuvers.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Blackman, S., Popoli, R.: Design and Analysis of Modern Tracking System. Artech House, Norwood (1999)
Chan, K., Lee, V., Leung, H.: Radar Tracking for Air Surveillance in a Stressful Environment Using a Fuzzy-gain Filter. IEEE Transactions on Aerospace and Electronic Systems, 80–89 (1997)
Julier, S.J., Uhlmann, J.K.: Unscented Filtering and Nonlinear Estimation. In: Proceedings of IEEE, pp. 401–422 (2004)
Julier, S.J., Uhlmann, J.K.: A New Method for the Nonlinear Transformation of Means and Covariance in Filters and Estimators. IEEE Transactions on Automatic Control, 477–482 (2000)
Wan, E.A., Vander, M.R.: The Unscented Kalman Filter for Nonlinear Estimation. In: Proceedings of Signal Processing, pp. 153–158 (2000)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Hu, Sq., Guo, Lw., Jing, Zl. (2005). Unscented Fuzzy Tracking Algorithm for Maneuvering Target. In: Wang, L., Jin, Y. (eds) Fuzzy Systems and Knowledge Discovery. FSKD 2005. Lecture Notes in Computer Science(), vol 3613. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11539506_88
Download citation
DOI: https://doi.org/10.1007/11539506_88
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-28312-6
Online ISBN: 978-3-540-31830-9
eBook Packages: Computer ScienceComputer Science (R0)