Abstract
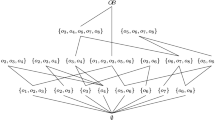
Significance of granular logic, including the operational rules, studying background, is presented in this paper. This closeness relation \(``\sim_{\lambda}"\) is quoted in granular logic,and the closeness relation \(``\sim_{\lambda}"\) quoted in granular logic is defined via logical truth values. Hence, we induce several new relative properties and inference rules in the granular logic with the closeness relation. The granular logical reasoning systems with the closeness relation \(``\sim_{\lambda}"\) are also established. And this paper proves a few real examples by deductive reasoning in the systems. Significance of granular logic with closeness relation ~ λ is also described in the paper.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Zadeh, L.A.: Fuzzy Sets and Information Granularity. In: Gupta, M., Ragade, R., Yager, R. (eds.) Advances in Fuzzy Set Theory and Applications, pp. 3–18. North-Holland, Amsterdam (1979)
Zadeh, L.A.: Some reflections on soft computing, granular computing and their roles in the conception, design and utilization of information/intelligent systems. In: Soft Computing, vol. 2, pp. 23–25. Springer, Berlin (1998)
Zadeh, L.A.: Toward a theory of fuzzy information granulation and its centrality in hunan reasoning and fuzzy logic. Fuzzy Sets and Systems 90, 111–127 (1997)
Chakraborty, M.K., Banerjee, M.: Rough logic with rough quantifiers. Warsaw University of Technology, ICS Research Report 49/93 (1993)
Pawlak, Z.: Rough sets – Theoretical aspects of reasoning about data. Kluwer Academic Publishers, Dordrecht (1991)
Liu, Q., Huang, Z.H.: G-Logic and Its Resolution Reasoning. Chinese Journal of Computer (In Chinese) 27(7), 865–873 (2004)
Liu, Q.: The OI-resolution of operator rough logic. In: Polkowski, L., Skowron, A. (eds.) RSCTC 1998. LNCS (LNAI), vol. 1424, p. 432. Springer, Heidelberg (1998)
Stepaniuk, J.: Rough Relations and Logics. In: Polkowski, L., Skowron, A. (eds.) Rough Sets in Knowledge Discovery I, pp. 248–260. Physica, Heideberg (1998)
Liu, Q.: λ-Level Rough Equality Relation and the Inference of Rough Paramodulation. In: Ziarko, W.P., Yao, Y. (eds.) RSCTC 2000. LNCS (LNAI), vol. 2005, pp. 462–469. Springer, Heidelberg (2001)
Skowron, A.: Toward intelligent systems: Calculi of information granules. In: Proc. of RSTGC 2001, Bulletin of International Rough Set Society, Japan, vol. 5(1/2), pp. 9–30 (2001)
Skowron, A., Stepaniuk, J.: Extracting patterns using information granules. In: Proc. of RSTGC 2001, Bulletin of International Rough Set Society, Japan, vol. 5(1/2), pp. 135–142 (2001)
Liu, Q., Liu, S.H., Zheng, F.: Rough logic and its applications in data mining. Journal of Software 12(3), 415–419 (2001)
Rasiowa, H., Skowron, A.: Rough concepts logic. In: Skowron, A. (ed.) SCT 1984. LNCS, vol. 208, pp. 288–297. Springer, Heidelberg (1985)
Lin, T.Y., Liu, Q.: First-order rough logic I: Approximate reasoning via rough sets. Fundamenta Informaticae 27(2-3), 137–154 (1996)
Wang, X.J.: Introduction for mathematical logic. Press of Beijing Uni., Beijing (1982)
Hamilton, A.G.: Logic For Mathematicians. Cambridge Uni. Press, London (1978)
Lin, T.Y.: Granular Computing on Binary Relations II: Rough Set Representations and Belief Functions. In: Skowron, A., Polkowski, L. (eds.) Rough Sets In Knowledge Discovery, pp. 121–140. Physica, Berlin (1998)
Lin, T.Y.: Granular Computing: Fuzzy Logic and Rough Sets. In: Zadeh, L.A., Kacprzyk, J. (eds.) Computing with Words, Information Intelligent Systems, vol. 1, pp. 183–200. Springer, Berlin (1999)
Yao, Y.Y., Yao, J.T.: Granular Computing as a Basis for Consistent Classification Problems. In: Proc. of PAKDD 2002 Workshop on Foundations of Data Mining, CIICM, Taiwan, vol. 5, pp. 101–106 (2002)
Liu, Q., Liu, Q.: Approximate Reasoning Based on Granular Computing in Granular Logic. In: Proc. of IEEE ICMLS 2002 (2002)
Liu, Q.: Granular Language and Its Reasoning, Data Mining and Knowledge Discovery: Theory, Tools, and Technology V. In: Proc. of SPIE 2003, pp. 279–287 (2003)
Liu, Q.: Granules and Applications of Granular Computing in Logical Reasoning (In Chinese). Journal of Computer Research and Development 41(4), 546–551 (2004)
Liu, Q.: Temporal Rough Logic and Its Application in Data Analysis. Journal of Fudan University (Natural Science) (In Chinese) 43(5), 852–855 (2005)
Orlowska, E.: A Logic of Indiscernibility Relation. In: Skowron, A. (ed.) SCT 1984. LNCS, vol. 208, pp. 177–186. Springer, Heidelberg (1985)
Yao, Y.Y., Liu, Q.: A Generalized Decision Logic in Interval-Set-Valued Information Table. In: Zhong, N., Skowron, A., Ohsuga, S. (eds.) RSFDGrC 1999. LNCS (LNAI), vol. 1711, pp. 285–294. Springer, Heidelberg (1999)
Lin, T.Y.: Granular Computing on Binary Relations-Analysis of Conflict and Chinese Wall Security Policy. In: Alpigini, J.J., Peters, J.F., Skowron, A., Zhong, N. (eds.) RSCTC 2002. LNCS (LNAI), vol. 2475, pp. 296–299. Springer, Heidelberg (2002)
Lin, T.Y.: Granular Computing on Binary Relations I: Data Mining and Neighborhood Systems. In: Skowron, A., Polkowski, L. (eds.) Rough Sets In Knowledge Discovery, pp. 107–121. Physica, Berlin (1998)
Zhang, L., Zhang, B.: The Quotient Space Theory of Problem Solving. In: Wang, G., Liu, Q., Yao, Y., Skowron, A. (eds.) RSFDGrC 2003. LNCS (LNAI), vol. 2639, pp. 11–15. Springer, Heidelberg (2003)
Yao, Y.Y.: Information granulation and Rough Set Approximation. International Journal of Intelligence Systems 16, 87–104 (2001)
Yao, Y.Y., Yao, J.T.: Granular Computing as a Basis for Consistent Classification Problems. In: Proc. of PAKDD 2002 Workshop on Foundations of Data Mining, CIICM, Taiwan, pp. 101–106 (2002)
Yao, Y.Y., Zhong, N.: Granular Computing Using Information Tables. In: Lin, T.Y., Yao, Y.Y., Zadeh, L.A. (eds.) Data Mining, Rough Sets and Granular Computing, pp. 102–124. Physica, Berlin (2002)
Yao, J.T., Yao, Y.Y.: Induction of Classification Rules by Granular Computing. In: Alpigini, J.J., Peters, J.F., Skowron, A., Zhong, N. (eds.) RSCTC 2002. LNCS (LNAI), vol. 2475, pp. 175–182. Springer, Heidelberg (2002)
Peters, J.F., Skowron, A., Suraj, Z., Borkowski, M., Rzasa, W.: Measures of Inclusion and closeness of Information Granules: A Rough Set Approach. In: Alpigini, J.J., Peters, J.F., Skowron, A., Zhong, N. (eds.) RSCTC 2002. LNCS (LNAI), vol. 2475, pp. 300–307. Springer, Heidelberg (2002)
Liau, C.-J.: Belief Reasoning, Revision and Fusion by Matrix Algebra. In: Tsumoto, S., Słowiński, R., Komorowski, J., Grzymała-Busse, J.W. (eds.) RSCTC 2004. LNCS (LNAI), vol. 3066, pp. 133–142. Springer, Heidelberg (2004)
Liu, Q.: Granules and Reasoning Based on Granular Computing. In: Chung, P.W.H., Hinde, C.J., Ali, M. (eds.) IEA/AIE 2003. LNCS(LNAI), vol. 2718, pp. 516–526. Springer, Heidelberg (2003)
Liau, C.-J.: Many-Valued Dynamic Logic for Qualitative Decision Theory. In: Zhong, N., Skowron, A., Ohsuga, S. (eds.) RSFDGrC 1999. LNCS (LNAI), vol. 1711, pp. 294–303. Springer, Heidelberg (1999)
Doherty, P., Lukaszewicz, W., Szalas, A.: Information Granules for Intelligent Knowledge Structures. In: Wang, G., Liu, Q., Yao, Y., Skowron, A. (eds.) RSFDGrC 2003. LNCS (LNAI), vol. 2639, pp. 405–412. Springer, Heidelberg (2003)
Skowron, A., Stepaniuk, J., Peters, J.F.: Approximation of Information Granule Sets. In: Ziarko, W.P., Yao, Y. (eds.) RSCTC 2000. LNCS (LNAI), vol. 2005, pp. 65–72. Springer, Heidelberg (2001)
Zadeh, L.A.: Information Granulation and Its Centrality. In: Polkowski, L., Skowron, A. (eds.) RSCTC 1998. LNCS (LNAI), vol. 1424, pp. 35–36. Springer, Heidelberg (1998)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Liu, Q., Wang, Q. (2005). Granular Logic with Closeness Relation \(``\sim_{\lambda}"\) and Its Reasoning. In: Ślęzak, D., Wang, G., Szczuka, M., Düntsch, I., Yao, Y. (eds) Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. RSFDGrC 2005. Lecture Notes in Computer Science(), vol 3641. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11548669_73
Download citation
DOI: https://doi.org/10.1007/11548669_73
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-28653-0
Online ISBN: 978-3-540-31825-5
eBook Packages: Computer ScienceComputer Science (R0)