Abstract
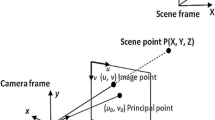
We investigate the problem of self-calibrating a camera, from multiple views of a planar scene. By self-calibrating, we refer to the problem of simultaneously estimate the camera intrinsic parameters and the Euclidean structure of one 3D plane. A solution is usually obtained by solving a non-linear system via local optimization, with the critical issue of parameter initialization, especially the focal length. Arguing that these five parameters are inter-dependent, we propose an alternate problem formulation, with only three d.o.f., corresponding to three parameters to estimate. In the light of this, we are concerned with global optimization in order to get a guaranteed solution, with the shortest response time. Interval analysis provides an efficient numerical framework, that reveals to be highly performant, with regard to both estimation accuracy and time-consuming.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Hartley, R., Zisserman, A.: Multiple View Geometry, 2nd edn. Cambridge University Press, Cambridge (2003)
Semple, J., Kneebone, G.: Algebraic Projective Geometry. Oxford Classic Series. Clarendon Press (1952) (reprinted, 1998)
Bougnoux, S.: From Projective to Euclidean Space under any Practical Situation, a Criticism of Self-Calibration. In: Proc. of the ICCV, Bombay, India, vol. 1, pp. 790–796 (1998)
Triggs, B.: Autocalibration from Planar Scenes. In: Proc. of the ECCV, Freiburg, Germany, vol. 2, pp. 89–105 (1998)
Malis, E., Cipolla, R.: Multi-view Constraints between Collineations: Application to Self-Calibration from Unknown Planar Structures. In: Proc. of the ECCV, Dublin, Ireland, vol. 2, pp. 610–624 (2000)
Gurdjos, P., Sturm, P.: Methods and Geometry for Plane-Based Self-Calibration. In: Proc. of the CVPR, Madison, Wisconsin, USA, vol. 1, pp. 491–496 (2003)
Jiang, G., Tsui, H., Quan, L.: Circular Motion Geometry Using Minimal Data. IEEE Trans. on PAMI 26, 721–731 (2004)
Knight, J., Zisserman, A., Reid, I.: Linear Auto-Calibration for Ground Plane Motion. In: Proc. of the CVPR, Madison, Wisconsin, USA, pp. 503–510 (2003)
Neumaier, A.: Introduction to Numerical Analysis. Cambridge University Press, Cambridge (2001)
Hansen, E.R., Walster, G.W.: Global Optimization Using Interval Analysis, 2nd edn. Marcel Dekker, New York (2003)
Fusiello, A., Benedetti, A., Farenzena, M., Busti, A.: Globally Convergent Autocalibration Using Interval Analysis. IEEE Trans. on PAMI 26, 1633–1638 (2004)
Golub, G., Loan, C.V.: Matrix computations, 3rd edn. John Hopkins University Press, Baltimore (1996)
Moore, R.E.: Interval Analysis. Prentice-Hall, Englewood Cliffs (1966)
Kearfott, R.B.: Rigorous Global Search: Continous Problems. Kluwer Academic Publishers, Dordrecht (1996)
Kanatani, K., Ohta, N.: Accuracy Bounds and Optimal Computation of Homography for Image Mosaicing Applications. In: Proc. of the ICCV, Kerkyra, Greece, vol. 1, pp. 73–78 (1999)
Sturm, P., Maybank, S.J.: On plane-based camera calibration: A general algorithm, singularities, applications. In: Proc. of the CVPR, Fort Collins, Colorado, USA, vol. 1, pp. 432–437 (1999)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Bocquillon, B., Gurdjos, P., Crouzil, A. (2006). Towards a Guaranteed Solution to Plane-Based Self-calibration. In: Narayanan, P.J., Nayar, S.K., Shum, HY. (eds) Computer Vision – ACCV 2006. ACCV 2006. Lecture Notes in Computer Science, vol 3851. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11612032_2
Download citation
DOI: https://doi.org/10.1007/11612032_2
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-31219-2
Online ISBN: 978-3-540-32433-1
eBook Packages: Computer ScienceComputer Science (R0)