Abstract
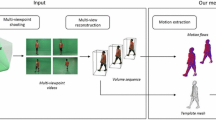
We show how to exploit temporal periodicity of moving objects to perform 3D reconstruction. The collection of period-separated frames serve as a surrogate for multiple rigid views of a particular pose of the moving target, thus allowing the use of standard techniques of multiview geometry. We motivate our approach using human motion capture data, for which the true 3D positions of the markers are known. We next apply our approach to image sequences of pedestrians captured with a camcorder. Applications of our proposed approach include 3D motion capture of natural and manmade periodic moving targets from monocular video sequences.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Cutler, R., Davis, L.: Robust real-time periodic motion detection, analysis, and applications. IEEE Transactions on Pattern Analysis and Machine Intelligence 22(8) (2000)
Faugeras, O.D.: What can be seen in three dimensions with an uncalibrated stereo rig? In: Sandini, G. (ed.) ECCV 1992. LNCS, vol. 588, pp. 563–578. Springer, Heidelberg (1992)
Förstner, W., Gülch, E.: A fast operator for detection and precise location of distinct points, corners and centres of circular features. In: ISPRS Intercommission Workshop, Interlaken (June 1987)
François, A.R.J., Medioni, G.G., Waupotitsch, R.: Mirror symmetry \(\Longrightarrow\) 2-view stereo geometry. Image and Vision Computing 21(2), 137–143 (2003)
Gårding, J.: Surface orientation and curvature from differential texture distortion. In: Proc. 5th Int’l Conf. on Computer Vision, Boston, pp. 733–739 (1995)
Gross, A.D., Boult, T.E.: Analyzing skewed symmetries. Int’l. Journal of Computer Vision 13(1), 91–111 (1994)
Hartley, R.I., Gupta, R., Chang, T.: Stereo from uncalibrated cameras. In: Proc. IEEE Conf. Comp. Vis. Patt. Recogn. (1992)
Hartley, R., Zisserman, A.: Multiple View Geometry in Computer Vision. Cambridge University Press, Cambridge (2000)
Kanade, T.: Recovery of the three-dimensional shape of an object from a single view. Artificial Intelligence 17, 409–460 (1981)
Kolmogorov, V., Zabih, R.: Computing visual correspondence with occlusions using graph cuts. In: Proc. 6th Int’l Conf. on Computer Vision, Vancouver (2001)
Liu, Y., Collins, R.T., Tsin, Y.: Gait sequence analysis using Frieze patterns. In: Proc. 7th Europ. Conf. Comput. Vision (2002)
Lowe, D.G.: Demo software: Invariant keypoint detector, http://www.cs.ubc.ca/spider/lowe/keypoints/
Koch, R., Pollefeys, M., Van Gool, L.: Self-calibration and metric reconstruction in spite of varying and unknown internal camera parameters. Int’l. Journal of Computer Vision 32(1), 7–25 (1999)
Malik, J., Rosenholtz, R.: Computing local surface orientation and shape from texture for curved surfaces. Int’l. Journal of Computer Vision 23(2), 149–168 (1997)
Mikolajczyk, K., Schmid, C.: An affine invariant interest point detector. In: European Conference on Computer Vision, pp. 128–142. Springer, Heidelberg (2002)
Song, Y., Goncalves, L., Perona, P.: Unsupervised learning of human motion. IEEE Trans. Pattern Analysis and Machine Intelligence 25(7), 814–827 (2003)
Torr, P.H.S., Murray, D.W.: The development and comparison of robust methods for estimating the fundamental matrix. Int. Journal of Computer Vision 24(3), 271–300 (1997)
Wills, J., Agarwal, S., Belongie, S.: What went where. In: Proc. IEEE Conf. Comput. Vision and Pattern Recognition, vol. 1, pp. 37–44 (2003)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Belongie, S., Wills, J. (2006). Structure from Periodic Motion. In: MacLean, W.J. (eds) Spatial Coherence for Visual Motion Analysis. SCVMA 2004. Lecture Notes in Computer Science, vol 3667. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11676959_2
Download citation
DOI: https://doi.org/10.1007/11676959_2
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-32533-8
Online ISBN: 978-3-540-32534-5
eBook Packages: Computer ScienceComputer Science (R0)