Abstract
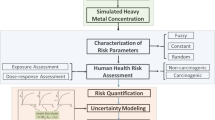
Subjective nature of system components makes the natural problems more complicated and harder to quantify. Thus, effective reflection of uncertainties, which is essential for generating reliable and realistic outcomes, has become a major concern for risk assessment. With the growing trend of fuzzy modeling and simulation of environmental problem, there is a need to develop a risk analysis approach which can use the fuzzy number output for characterization of risk. This study has been done to fulfil that need. Integration of system simulation and risk analysis using fuzzy approach allowed to incorporate system modelling uncertainty and subjective risk criteria. In this study, an integrated fuzzy relation analysis (IFRA) model is proposed for risk assessment involving multiple criteria. Model is demonstrated for a multi-components groundwater contamination problem. Results reflect uncertainties presented as fuzzy number for different modelling inputs obtained from fuzzy system simulation. Integrated risk can be calculated at different membership level which is useful for comprehensively evaluating risks within an uncertain system containing many factors with complicated relationship. It has been shown that a broad integration of fuzzy system simulation and fuzzy risk analysis is possible.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Abebe, A.J., Guinot, V., Solomatine, D.P.: Fuzzy alpha-cut vs. Monte Carlo techniques in assessing uncertainty in model parameters. In: Proc. 4th Int. Conf. Hydroinformatics, Iowa (2000)
Dong, W., Shah, H.C.: Vertex Method for Computing Functions of Fuzzy Variables. Fuzzy Sets and Systems 24, 65–78 (1987)
Dou, C., Woldt, W., Bogardi, I., Dahab, M.: Steady state groundwater flow and simulation with imprecise parameters. Water Resour. Res. 31(11), 2709–2719 (1995)
Dou, C., Woldt, W., Bogardi, I., Dahab, M.: Numerical Solute Transport Simulation using Fuzzy Sets Approach. J. Contaminant Hydrology 27, 107–126 (1997)
Kaluarachchi, J.J., Parker, J.C.: Modeling multicomponent organic chemical transport in three-fluid-phase porous media. J. Contam. Hydrol. 5, 349–374 (1990)
Katyal, A.K., Parker, J.C.: An adaptive solution domain algorithm for solving multiphase flow equations. Computers & Geosciences 18, 1–9 (1992)
Kumar, V., Schuhmacher, M.: Fuzzy uncertainty analysis in system modeling. In: Proceeding of ESCAPE –15, Barcelona, Spain, pp. 391–396 (2005)
Hanss, M., Willner, K.: On using fuzzy arithmetic to solve problems with uncertain model parameters. In: Proc. of the Euromech 405 Colloquium, Valenciennes, France, pp. 85–92 (1999)
Hanss, M.: The transformation method for the simulation and analysis of systems with uncertain parameters. Fuzzy Sets and Systems 130–3, 277–289 (2002)
Huang, G.H., Chen, Z., Tontiwachwuthikul, P., Chakma, A.: Environmental Risk Assessment for Underground Storage Tanks Through an Interval Parameter Fuzzy Relation Analysis. Energy Sources 21(1), 75–96 (1999)
Pedrycz, W.: Fuzzy sets in pattern recognition. Pattern Recognition 23, 121–146 (1990)
Sauty, J.P.: An analysis of hydrodispersive transfer in aquifers. Water Resour. Res. 16-1, 145–158 (1980)
Zadeh, L.: Fuzzy algorithms. Information and Control 12, 94–102 (1968)
Zadeh, L.A.: Fuzzy Sets and Their Application to Pattern Classification And Clustering Analysis. In: Van Ryzin, J. (ed.) Classification and Clustering, pp. 251–299. Academic Press, London (1977)
Zadeh, L.: Fuzzy logic. IEEE Computer 1(14), 83–93 (1988)
Zimmermann, H.J.: Fuzzy Set Theory and Its Applications, 2nd edn. Kluwer Academic Publishers, Boston (1991)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Kumar, V., Schuhmacher, M., García, M. (2006). Integrated Fuzzy Approach for System Modeling and Risk Assessment. In: Torra, V., Narukawa, Y., Valls, A., Domingo-Ferrer, J. (eds) Modeling Decisions for Artificial Intelligence. MDAI 2006. Lecture Notes in Computer Science(), vol 3885. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11681960_23
Download citation
DOI: https://doi.org/10.1007/11681960_23
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-32780-6
Online ISBN: 978-3-540-32781-3
eBook Packages: Computer ScienceComputer Science (R0)