Simulation Studies of On-Line Identification of Complex Processes with Neural Networks

Abstract

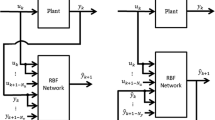
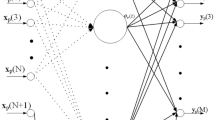
This paper analyzes various formulations for the recursive training of neural networks that can be used for identifying and optimizing nonlinear processes on line. The study considers feedforward type networks (FFNN) adapted by three different methods: inverse Hessian matrix approximation, calculation of the inverse Hessian matrix using a Gauss-Newton recursive sequential algorithm, and calculation of the inverse Hessian matrix in a recursive type Gauss-Newton algorithm. The study is completed using two network structures that are linear in the parameters: a radial basis network and a principal components network, both trained using a recursive least squares algorithm. The corresponding algorithms and a comparative test consisting of the on-line estimation of a reaction rate are detailed. The results indicate that all the structures were capable of converging satisfactorily in a few iteration cycles, FFNN type networks showing better prediction capacity, but the computational effort of the recursive algorithms is greater.