Abstract
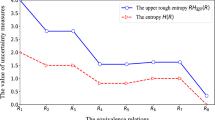
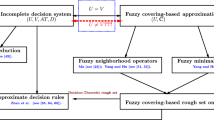
This paper presents a general framework for the study of covering-based rough fuzzy sets in which a fuzzy set can be approximated by some elements in a covering of the universe of discourse. Some basic properties of the covering-based lower and upper approximation operators are examined. The concept of reduction of a covering is also introduced. By employing the discrimination matric of the covering, we provide an approach to find the reduct of a covering of the universe. It is proved that the reduct of a covering is the minimal covering that generates the same covering-based fuzzy lower (or upper) approximation operator, so this concept is also a technique to get rid of redundancy in data mining. Furthermore, it is shown that the covering-based fuzzy lower and upper approximations determine each other.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Pawlak, Z.: Rough sets. International Journal of Computer and Information Science 11(5), 341–356 (1982)
Pawlak, Z.: Rough Sets: Theoretical Aspects of Reasoning about Data. Kluwer Academic Publishers, Boston (1991)
Skowron, A., Stepaniuk, J.: Tolerance approximation spaces. Fundam. Inform. 27, 245–253 (1996)
Yao, Y.Y.: Constructive and algebraic methods of theory of rough sets. Information Sciences 109, 21–47 (1998)
Slowinski, R., Vanderpooten, D.: A generalized definition of rough approximation based on similarity. IEEE Trans. Data Knowledge Eng. 2, 331–336 (2000)
Yao, Y.Y.: Relational interpretations of neighborhood operators and rough set approximation operators. Information Sciences 101, 239–259 (1998)
Yao, Y.Y., Lin, T.Y.: Generalization of rough sets using modal logic. Intelligent Automation and Soft computing: an International Journal 2, 103–120 (1996)
Zakowski, W.: Approximations in the space (U, ∏ ). Demonstration Mathematica 16, 761–769 (1983)
Bonikowski, Z., Bryniarski, E., Wybraniec, U.: Extensions and intentions in the rough set theory. Information Sciences 107, 149–167 (1998)
Zhu, W., Wang, F.Y.: Reduction and axiomization of covering generalized rough sets. Information Sciences 152, 217–230 (2003)
Dubois, D., Prade, H.: Rough fuzzy sets and fuzzy rough sets. International Journal of General System 17, 191–208 (1990)
Dubois, D., Prade, H.: Putting rough sets and fuzzy sets together. In: Slowinski, R. (ed.) Intelligent Decision Support: Handbook of Applications and Advances of the Rough Sets Theory, pp. 203–232. Kluwer Academic Publishers, Dordrecht (1992)
Inuiguchi, M., Tanino, T.: New fuzzy rough sets based on certainty qualification. In: Pal, S.K., Polkowski, L., Skowron, A. (eds.) Rough-Neural Computing: Techniques for Computing with Words, pp. 277–296. Springer, Heidelberg (2004)
Mi, J.S., Leung, Y., Wu, W.Z.: An uncertainty measure in partition-based fuzzy rough sets. International Journal of General Systems 34, 77–90 (2005)
Mi, J.S., Zhang, W.X.: An axiomatic characterization of a fuzzy generalization of rough sets. Information Sciences 160(1-4), 235–249 (2004)
Wu, W.Z., Mi, J.S., Zhang, W.X.: Generalized fuzzy rough sets. Information Sciences 151, 263–282 (2003)
Slowinski, R., Stefanowski, J.: Medical information systems–problems with analysis and way of solution. In: Pal, S.K., Skowron, A. (eds.) Rough Fuzzy Hybridization: A New Trend in Decision-making, pp. 301–315. Springer, Singapore (1999)
Polkowski, L.: Rough Sets. Mathematical Foundations. Physica–Verlag, Heidelberg (2002)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Feng, T., Mi, J., Wu, W. (2006). Covering-Based Generalized Rough Fuzzy Sets. In: Wang, GY., Peters, J.F., Skowron, A., Yao, Y. (eds) Rough Sets and Knowledge Technology. RSKT 2006. Lecture Notes in Computer Science(), vol 4062. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11795131_30
Download citation
DOI: https://doi.org/10.1007/11795131_30
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-36297-5
Online ISBN: 978-3-540-36299-9
eBook Packages: Computer ScienceComputer Science (R0)