Abstract
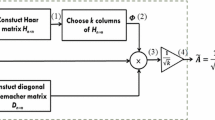
Given an m ×n matrix A and an integer k less than the rank of A, the “best” rank k approximation to A that minimizes the error with respect to the Frobenius norm is A k , which is obtained by projecting A on the top k left singular vectors of A. While A k is routinely used in data analysis, it is difficult to interpret and understand it in terms of the original data, namely the columns and rows of A. For example, these columns and rows often come from some application domain, whereas the singular vectors are linear combinations of (up to all) the columns or rows of A. We address the problem of obtaining low-rank approximations that are directly interpretable in terms of the original columns or rows of A. Our main results are two polynomial time randomized algorithms that take as input a matrix A and return as output a matrix C, consisting of a “small” (i.e., a low-degree polynomial in k, 1/ε, and log(1/δ)) number of actual columns of A such that
||A–CC + A|| F ≤(1+ε) ||A–A k || F
with probability at least 1–δ. Our algorithms are simple, and they take time of the order of the time needed to compute the top k right singular vectors of A. In addition, they sample the columns of A via the method of “subspace sampling,” so-named since the sampling probabilities depend on the lengths of the rows of the top singular vectors and since they ensure that we capture entirely a certain subspace of interest.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Bhatia, R.: Matrix Analysis. Springer, New York (1997)
Deshpande, A., Rademacher, L., Vempala, S., Wang, G.: Matrix approximation and projective clustering via volume sampling. In: Proceedings of the 17th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 1117–1126 (2006)
Deshpande, A., Vempala, S.: Adaptive sampling and fast low-rank matrix approximation. Technical Report TR06-042, Electronic Colloquium on Computational Complexity (March 2006)
Drineas, P., Frieze, A., Kannan, R., Vempala, S., Vinay, V.: Clustering in large graphs and matrices. In: Proceedings of the 10th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 291–299 (1999)
Drineas, P., Kannan, R., Mahoney, M.W.: Fast Monte Carlo algorithms for matrices I: Approximating matrix multiplication. SIAM Journal on Computing (to appear)
Drineas, P., Kannan, R., Mahoney, M.W.: Fast Monte Carlo algorithms for matrices II: Computing a low-rank approximation to a matrix. SIAM Journal on Computing (to appear)
Drineas, P., Kannan, R., Mahoney, M.W.: Fast Monte Carlo algorithms for matrices III: Computing a compressed approximate matrix decomposition. SIAM Journal on Computing (to appear)
Drineas, P., Mahoney, M.W., Muthukrishnan, S.: Polynomial time algorithm for column-row based relative-error low-rank matrix approximation. Technical Report 2006-04, DIMACS (March 2006)
Drineas, P., Mahoney, M.W., Muthukrishnan, S.: Sampling algorithms for ℓ. regression and applications. In: Proceedings of the 17th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 1127–1136 (2006)
Frieze, A., Kannan, R., Vempala, S.: Fast Monte-Carlo algorithms for finding low-rank approximations. In: Proceedings of the 39th Annual IEEE Symposium on Foundations of Computer Science, pp. 370–378 (1998)
Frieze, A., Kannan, R., Vempala, S.: Fast Monte-Carlo algorithms for finding low-rank approximations. Journal of the ACM 51(6), 1025–1041 (2004)
Golub, G.H., Van Loan, C.F.: Matrix Computations. Johns Hopkins University Press, Baltimore (1989)
Har-Peled, S.: Low rank matrix approximation in linear time (manuscript, January 2006)
Horn, R.A., Johnson, C.R.: Matrix Analysis. Cambridge University Press, New York (1985)
Kuruvilla, F.G., Park, P.J., Schreiber, S.L.: Vector algebra in the analysis of genome-wide expression data. Genome Biology, 3: research 0011.1–0011.11 (2002)
Lin, Z., Altman, R.B.: Finding haplotype tagging SNPs by use of principal components analysis. American Journal of Human Genetics 75, 850–861 (2004)
Nashed, M.Z. (ed.): Generalized Inverses and Applications. Academic Press, New York (1976)
Paschou, P., Mahoney, M.W., Kidd, J.R., Pakstis, A.J., Gu, S., Kidd, K.K., Drineas, P.: Intra- and inter-population genotype reconstruction from tagging SNPs (manuscript submitted for publication)
Rademacher, L., Vempala, S., Wang, G.: Matrix approximation and projective clustering via iterative sampling. Technical Report MIT-LCS-TR-983, Massachusetts Institute of Technology, Cambridge, MA (March 2005)
Rudelson, M., Vershynin, R.: Approximation of matrices (manuscript)
Vershynin, R.: Coordinate restrictions of linear operators in \(l_2^n\) (manuscript)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Drineas, P., Mahoney, M.W., Muthukrishnan, S. (2006). Subspace Sampling and Relative-Error Matrix Approximation: Column-Based Methods. In: Díaz, J., Jansen, K., Rolim, J.D.P., Zwick, U. (eds) Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques. APPROX RANDOM 2006 2006. Lecture Notes in Computer Science, vol 4110. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11830924_30
Download citation
DOI: https://doi.org/10.1007/11830924_30
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-38044-3
Online ISBN: 978-3-540-38045-0
eBook Packages: Computer ScienceComputer Science (R0)