Abstract
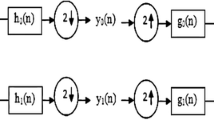
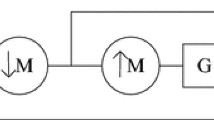
This paper focuses on fuzzy image denoising techniques. In particular, we investigate the usage of fuzzy set theory in the domain of image enhancement using wavelet thresholding. We propose a simple but efficient new fuzzy wavelet shrinkage method, which can be seen as a fuzzy variant of a recently published probabilistic shrinkage method [1] for reducing adaptive Gaussian noise from digital greyscale images. Experimental results show that the proposed method can efficiently and rapidly remove additive Gaussian noise from digital greyscale images. Numerical and visual observations show that the performance of the proposed method outperforms current fuzzy non-wavelet methods and is comparable with some recent but more complex wavelets methods. We also illustrate the main differences between this version and the probabilistic version and show the main improvements in comparison to it.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Pižurica, A., Philips, W.: Estimating the probability of the presence of a signal of interest in multiresolution single- and multiband image denoising. IEEE Transactions on Image Process. 15(3), 654–665 (2006)
Resnikoff, H.L., Wells, R.O.: Wavelet Analysis: The Scalable Structure of Information. Springer, Heidelberg (1998)
Donoho, D.: Denoising by soft-thresholding. IEEE Transactions on Information Theory 41(5), 613–627 (1995)
Donoho, D., Johnstone, I.: Adapting to unknown smoothness via wavelet shrinkage. Journal of the American Statistical Association 90, 1200–1224 (1995)
Chang, S., Yu, B., Vetterli, M.: Adaptive wavelet thresholding for image denoising and compression. IEEE Transactions on Image Processing 9(9), 1532–1546 (2000)
Hansen, M., Yu, B.: Wavelet thresholding via mdl for natural images. IEEE Transactions on Information Theory 46(8), 1778–1788 (2000)
Simoncelli, E., Adelson, E.: Noise removal via Bayesian wavelet coring. In: Proceedings IEEE International Conference on Image Processing (ICIP 1996), Lausanne, Switserland, pp. 379–382 (1996)
Moulin, P., Liu, J.: Analysis of multiresolution image denoising schemes using generalized gaussian and complexity priors. IEEE Transactions on Information Theory 45(4), 909–919 (1999)
Pižurica, A., Philips, W., Lemahieu, I., Acheroy, M.: A joint inter- and intrascale statistical model for Bayesian wavelet based image denoising. IEEE Transactions on Image Processing 11(5), 545–557 (2002)
Portilla, J., Strela, V., Wainwright, M., Simoncelli, E.: Image denoising using gaussian scale mixtures in the wavelet domain. IEEE Transactions on Image Processing 12(11), 1338–1351 (2003)
Vidakovic, B.: Nonlinear wavelet shrinkage with bayes rules and bayes factors. Journal of the American Statistical Association 93, 173–179 (1998)
Chipman, H., Kolaczyk, E., McCulloch, R.: Adaptive Bayesian wavelet shrinkage. Journal of the American Statistical Association 92, 1413–1421 (1997)
Sendur, L., Selesnick, I.: Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency. IEEE Transactions on Signal Processing 50(11), 2744–2756 (2002)
Crouse, M., Nowak, R., Baranuik, R.: Wavelet-based statistical signal processing using hidden Markov models. IEEE Transactions on Signal Processing 46(4), 886–902 (1998)
Romberg, J., Choi, H., Baraniuk, R.: Bayesian tree-structured image modeling using wavelet-domain hidden markov models. IEEE Transactions on Image Processing 10, 1056–1068 (2001)
Malfait, M., Roose, D.: Wavelet-based image denoising using a markov random field a priori model. IEEE Transactions on Image Processing 6(4), 549–565 (1997)
Jansen, M., Bultheel, A.: Empirical Bayes approach to improve wavelet thresholding for image noise reduction. Journal of the American Statistical Association 96(454), 629–639 (2001)
Mihcak, M., Kozintsev, I., Ramchandran, K., Moulin, P.: Low complexity image denoising based on statistical modeling of wavelet coefficients. IEEE Signal Processing Letters 6, 300–303 (1999)
Fan, G., Xia, X.: Image denoising using local contextual hidden markov model in the wavelet domain. IEEE Signal Processing Letters 8(5), 125–128 (2001)
Fan, G., Xia, X.: Improved hidden Markov models in the wavelet domain. IEEE Transactions on Signal Processing 49, 115–120 (2001)
Kerre, E.E.: Fuzzy sets and approximate Reasoning. Xian Jiaotong University Press (1998)
Tizhoosh, H.R.: Fuzzy-Bildverarbeitung: Einführung in Theorie und Praxis. Springer, Heidelberg (1997)
Zadeh, L.A.: Fuzzy Sets. Information and Control 8(3), 338–353 (1965)
Zadeh, L.A.: Fuzzy logic and its application to approximate reasoning. Information Processing 74, 591–594 (1973)
Donoho, D.L., Johnstone, I.M.: Ideal spatial adaptation by wavelet shrinkage. Biometrika 81, 425–455 (1994)
Van De Ville, D., Nachtegael, M., Van der Weken, D., Kerre, E.E., Philips, W.: Noise reduction by fuzzy image filtering. IEEE Transactions on Fuzzy Systems 11(4), 429–436 (2003)
Schulte, S., De Witte, V., Nachtegael, M., Van der Weken, D., Kerre, E.E.: Fuzzy Random Impulse Noise Reduction Method. Fuzzy Sets and Systems (submitted) (2006)
Wang, J.H., Chiu, H.C.: An adaptive fuzzy filter for restoring highly corrupted images by histogram estimation. Proceedings of the National Science Council -Part A 23, 630–643 (1999)
Farbiz, F., Menhaj, M.B., Motamedi, S.A.: Edge Preserving Image Filtering based on Fuzzy Logic. In: Proceedings of the 6th EUFIT conference, pp. 1417–1421 (1998)
Kwan, H.K., Cai, Y.: Fuzzy filters for image filtering. In: Proceedings of Circuits and Systems (MWSCAS 2002). The 2002 45th Midwest Symposium, pp. III-672–III-675 (2002)
Xu, H., Zhu, G., Peng, H., Wang, D.: Adaptive fuzzy switching filter for images corrupted by impulse noise. Pattern Recognition Letters 25, 1657–1663 (2004)
Tolt, G., Kalaykov, I.: Fuzzy-similarity-based Noise Cancellation for Real-time Image Processing. In: Proceedings of the 10th IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), vol. 1, pp. 15–18
Tolt, G., Kalaykov, I.: Fuzzy-Similarity-Based Image Noise Cancellation. In: Pal, N.R., Sugeno, M. (eds.) AFSS 2002. LNCS, vol. 2275, pp. 408–413. Springer, Heidelberg (2002)
Kuo, Y.H., Lee, C.S., Chen, C.L.: High-stability AWFM filter for signal restoration and its hardware design. Fuzzy Sets and Systems 114(2), 185–202 (2000)
Şendur, L., Selesnick, I.W.: Bivariate Shrinkage Functions for Wavelet-based Image Denoising. IEEE Transactions on Signal Processing 50(11), 2744–2756 (2002)
Balster, E.J., Zheng, Y.F., Ewing, R.L.: Feature-based wavelet shrinkage algorithm for image denoising. IEEE Transactions on Image Process 14(3), 2024–2039 (2005)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Schulte, S., Huysmans, B., Pižurica, A., Kerre, E.E., Philips, W. (2006). A New Fuzzy-Based Wavelet Shrinkage Image Denoising Technique. In: Blanc-Talon, J., Philips, W., Popescu, D., Scheunders, P. (eds) Advanced Concepts for Intelligent Vision Systems. ACIVS 2006. Lecture Notes in Computer Science, vol 4179. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11864349_2
Download citation
DOI: https://doi.org/10.1007/11864349_2
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-44630-9
Online ISBN: 978-3-540-44632-3
eBook Packages: Computer ScienceComputer Science (R0)